Esta página está en construcción: perdonen los errores y temas inacabados.
This page is being developed: I am sorry for errors and unfinished subjects.
Otras espirales
Tras descubrir y estudiar nuestra espiral harmónica, nos lanzamos a estudiar otras siguiendo sus pasos, sabiendo bien que no hacemos mas que redescubrir lo ya descubierto. Descubrir sería así algo como destapar lo que estaba cubierto (cubierto por nuestra ignorancia...)
La espiral lineal (conocida como de Arquímedes)
0. Ecuación.
En este caso tanto el radio como el ángulo de las coordenadas polares de cada punto de la espiral, son proporcionales al intervalo con una cierta frecuencia determinada. Eligiendo la octava, que designamos por oc., asignamos asimismo cada una de ellas a una vuelta completa. De modo que el ángulo, en radianes, vale
q =2p ln( f / f0 ) / ln (2)
ya que para f / f0 =2, una octava, el ángulo vale en efecto, una vuelta, 2p radianes.
A su vez, el radio lo elegimos arbitrariamente también proporcional al intervalo logarítmico.
r =r0 ln( f / f0 ) / ln (2)
de modo que para la primera octava-vuelta, tenemos r =r0 el radio es igual a un radio inicial arbitrario.
Eliminando la variable intervalo entre ambas ecuaciones paramétricas, se obtiene la ecuación en coordenadas polares:
r =r0 . q
con el parámetro arbitrario r0 que depende de las unidades de dibujo. y que 'abre' más o menos la espiral.
La espiral obtenida no es ya logarítmica, y presenta volutas equidistantes al crecer el ángulo.
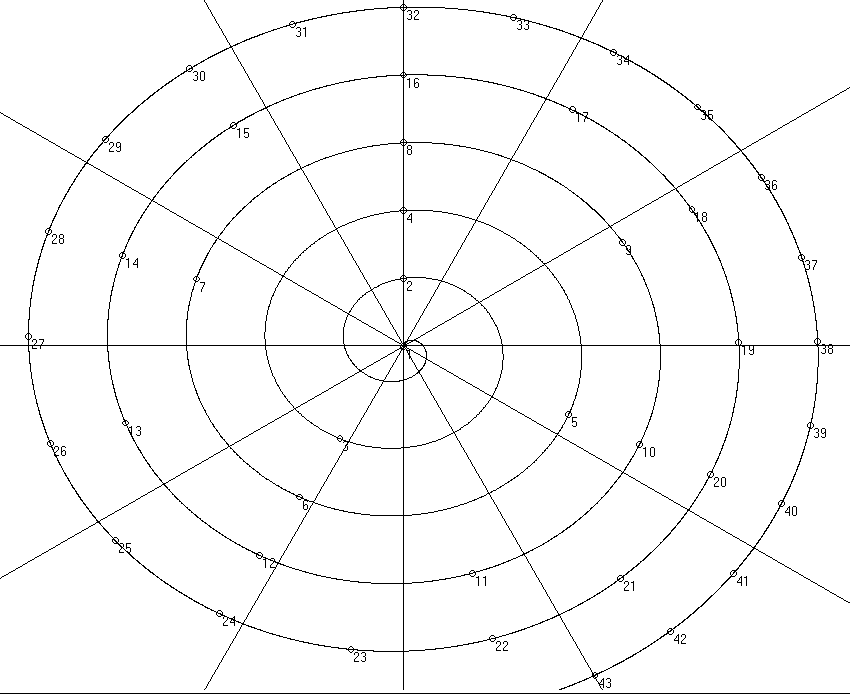
1. Según estas definiciones, radio y ángulo crecen proporcionalmente, ya que representan esencialmente el mismo parámetro: el intervalo con el fundamental. Pero es el ángulo el que resulta más informativo e intuitivo, ya que se visualiza bien la octava como una vuelta, y los semitonos temperados sobre uno de12 radios igualmente espaciados en el círculo (pero no ya sobre la curva en este caso).
Longitud de la curva
El elemento de curva, cuya longitud es ds, forma, como hipotenusa, un triángulo rectángulo con dos catetos, el elemento de arco r dq y el crecimiento diferencial de radio, dr (véase figura anterior). lo que conduce a la expresión de la longitud del elemento de curva:
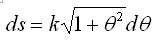
siendo k =r0 /2p
Integrando ese elemento entre dos puntos de ángulos q1 y q: obtenemos la longitud de la curva entre dos ángulos:
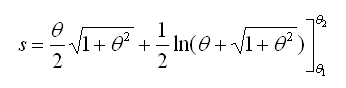
expresión más complicada que en la primera espiral.
Su derivada ds, demuestra que es una función ligeramente decreciente con el ángulo q, y converge hacia él cuando es grande, al perder entonces importancia el sumando 1 bajo la raíz. En cuanto a la frecuencia, en la figura vemos que por cada harmónico en una espira hay dos en la siguiente. Sólo que la curva es cada vez más plana de modo que la distancia sobre ella crece menos rápidamente que el doble.
En cambio encontramos la propiedad de que las vueltas o espiras están a igual distancia unas de otras. Todos los harmónicos múltiplos de 2, por ejemplo, distan lo mismo de sus vecinos en la serie. Se prueba fácilmente. Para dos frecuencias en proporción fija:
r2-r1 =r0 ln( f2 / f1 ) / ln (2)
expresión constante si el neperiano del cociente de las frecuencias lo es. De modo que para un intervalo constante, la distancia entre espiras, la diferencia de los radios, es constante. Así se aprecia en la figura. Esta distancia es, para cada tipo de curva igual. para las curvas de octavas, encontramos, justamente que esa distancia es precisamente r =r0 ln ( 2. f0 / f0 ) / ln (2) = r0 la distancia entre el origen y la primera octava.
La espiral inversa
Si prolongamos esta segunda espiral con las frecuencias e intervalos descendentes desde la frecuencia de partida, f0 , encontramos la rama homóloga de la ya vista, cuya ecuación es la misma:
r =r0 /2p . q
pero extendiéndola a valores de r y q negativos. Obviamente un valor negativo del primero corresponde a un sentido opuesto del vector sobre su dirección, de modo que al prolongar q hacia valores negativos, también lo hace r con lo que la expresión anterior es en efecto válida para esta otra rama, como adelantábamos.
La rama negativa, llamémosla así, comienza como su homóloga por un valor pequeño y crece con el ángulo. se desarrolla simétricamente a la otra respecto al eje horizontal (esto debido al comienzo del ángulos en el eje vertical y crecimiento de ángulos hacia la derecha, en el del reloj. Las octavas con la referencia aparecen ahora abajo (acordemente con el sentido descendente de los intervalos) .