La espiral harmónica La idea de esta espiral nos surgió hace tiempo, como muestra la leyenda en el dibujo.Esta página está en construcción: perdonen los errores y temas inacabados.
This page is being developed: I am sorry for errors and unfinished subjects.
Si situamos sobre un plano puntos relacionados con los
harmónicos que componen un sonido, cuyas proporciones relativas (cociente de
frecuencias con el primero o fundamental) son, como es sabido, 1,2 3, 4, 5,
6.. etc., de modo que con respecto a un punto, el centro, cada harmónico viene
representado por un punto en coordenadas polares (1º:distancia
al centro, 2º:ángulo con la horizontal a la derecha del centro, creciendo el
ángulo en sentido arbitrariamente positivo tomado como el opuesto al giro del
reloj) de modo que el radio es proporcional a la frecuencia, y el
ángulo proporcional al intervalo logarítmico
(octavas, semitonos, cents) con el fundamental (representado a su vez por el
centro, radio nulo, pero
de modo que una octava corresponda a una vuelta completa (2p
radianes o 360º sexagesimales) obtenemos una serie de puntos sobre una curva
que resulta ser una espiral logarítmica. La curva completa se obtiene
representando todos los intervalos posibles con el fundamental, no sólo sus
harmónicos.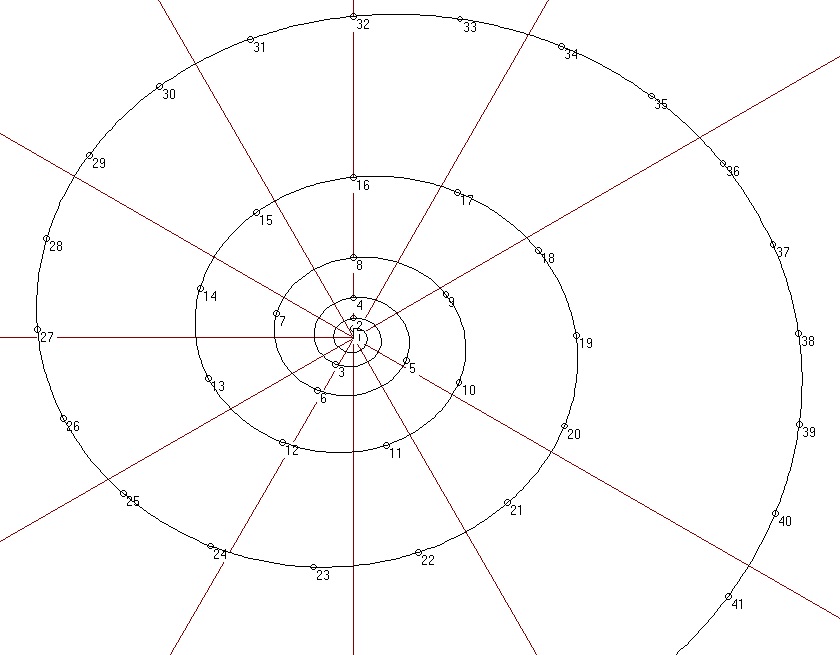
Si llamamos DO al primer harmónico, el fundamental, los demás corresponden a notas que nombraremos siguiendo la escala de comas Hölder, obteniéndose así:
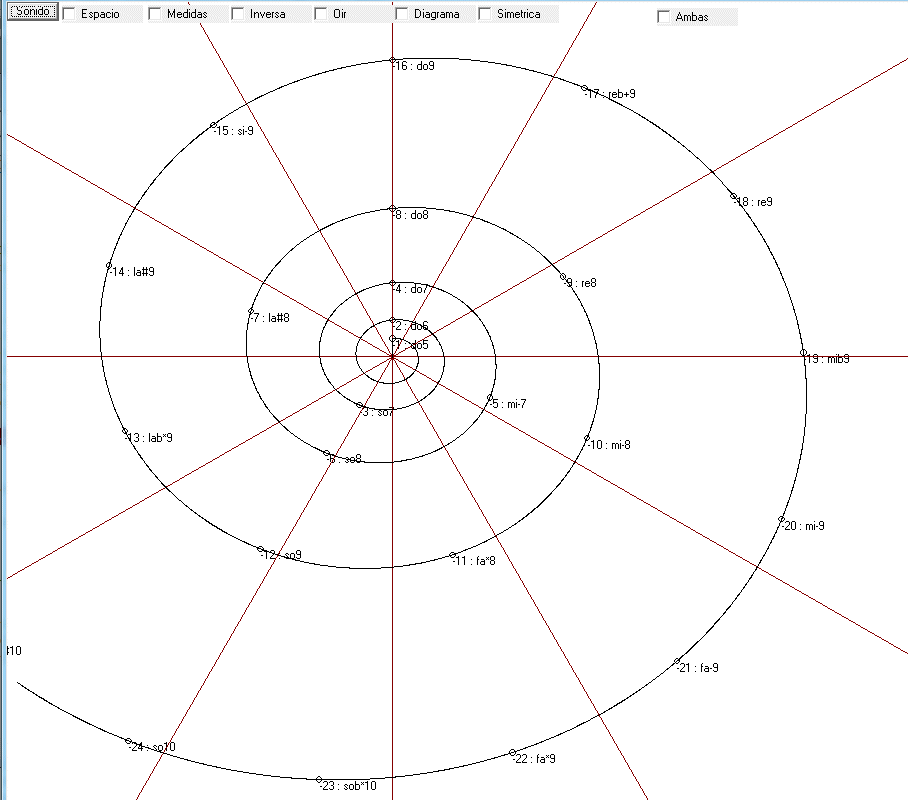
O
Esta curva, que definimos así, la hemos llamado Espiral
Harmónica. Posee esta espiral propiedades interesantes y bellas, que
investigamos a continuación.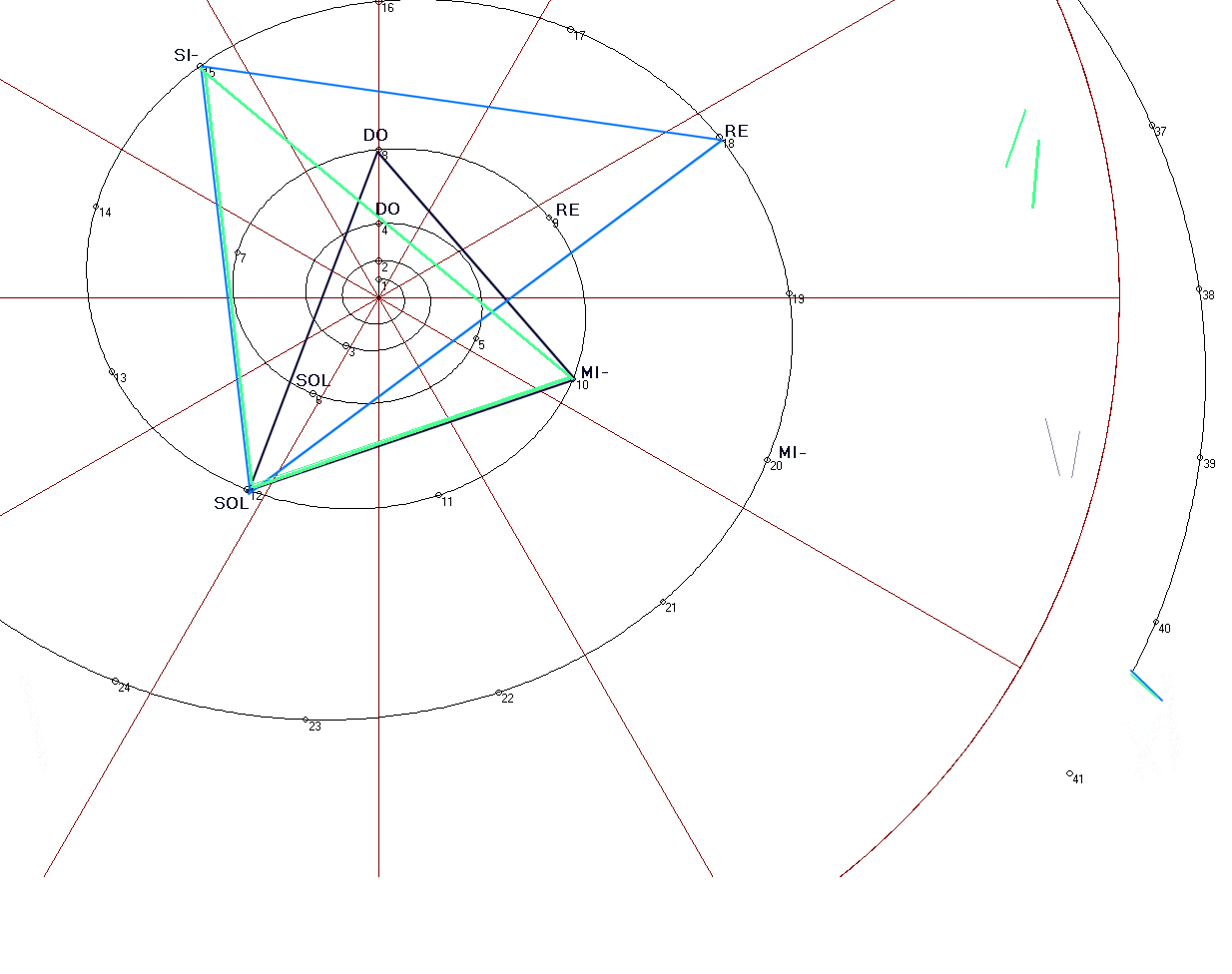
0. Ecuación.
Según hemos descrito antes, tanto el radio como el ángulo de las coordenadas polares de cada punto de la espiral son respectivamente proporcionales a la frecuencia y a su intervalo con una cierta frecuencia determinada. Intervalo expresado en las habituales unidades de tipo logarítmico, las usuales octavas semitonos y cents. Eligiendo la octava, que designamos por oc., asignamos arbitraria (pero lógica) mente cada una de ellas a una vuelta completa. De modo que el ángulo, en radianes, vale
q =2p ln( f / f0 ) / ln (2)
ya que para f / f0 =2, una octava, el ángulo vale en efecto, una vuelta, 2p radianes.
A su vez, el radio lo elegimos arbitrariamente proporcional al cociente de frecuencias, en este caso.
r =r0 f / f0
de modo que para la primera octava-vuelta, f = f0 , tenemos r =r0 el radio es igual a un radio inicial arbitrario.
Eliminando la variable intervalo entre ambas ecuaciones paramétricas,
ln(r / r0 ) = ln ( f / f0 )
q = ln (r / r0 )
se obtiene la ecuación en coordenadas polares:
ln(r / r0 ) = ln (2). q/ /2p
de donde
r =r0 . e aq con a = ln (2) /2p = 0.11
que contiene los parámetros arbitrarios r0 que depende de las unidades de dibujo. y que 'abre' más o menos la espiral; y a , que regula cómo de confrontan o se avecinan los harmónicos entre sí. El valor dado es el correspondiente a las octavas enfrentadas, 2, como muestra la figura. Las instrucciones del programa que dibuja la espiral aparecen a continuación. La constante '2', para octavas está ampliada la variable INTERVUEL: (3/2 para quintas, 9/8 para tonos, etc.).
|
KATETA = 2 * PI / Log
(INTERVUEL) KAESE = KATETA * RO0 / frecuencia0 ro = KAESE / KATETA * frecuencia ' TETA = TETA0 + KATETA * Log(frecuencia / frecuencia0) |
|
Ecuaciones en VisualBasíc para dibujar los puntos de la espiral. |
1. Debido a esa proporcionalidad entre radio y exponencial del ángulo, se trata de una espiral logarítmica, curva muy conocida, empleada por ejemplo en las volutas de los capiteles jónicos griegos.
2. Quedan en el mismo radio octavas de un mismo sonido, reflejando así el parentesco fundamental matemático (2,4,8,) y perceptivo (consonancia)
3. La curva se prolonga infinitamente para frecuencias más bajas que la de referencia, llegando al origen para frecuencia cero.
4. Las distancias sobre la curva entre harmónicos son iguales, representando así el intervalos lineal (en hercios o vibraciones por segundo). La escala depende, claro, de la frecuencia del fundamental. Las distancias entre sus harmónicos representan esa diferencia de frecuencias (para 100 hz, tenemos harmónicos de frecuencias 200, 300, 400, etc.). Se demuestra esta propiedad sencillamente:
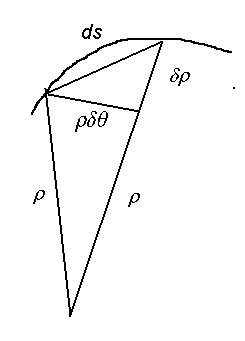 El
elemento de curva ds tiene una longitud, como hipotenusa del
triángulo de la figura:
El
elemento de curva ds tiene una longitud, como hipotenusa del
triángulo de la figura:
ds 2 = dr 2 + (rdq) 2
lo que deviene usando r =r0 . e aq y dr =a r0 . e aq . dq =a r . dq
ds 2 = r 2 (a 2 + 1) dq 2
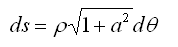
fórmula que expresa la proporcionalidad de la longitud del elemento de espiral con el radio vector, con un parámetro dependiente de a .
Pero el radio vector es proporcional a la frecuencia, por definición. Y así, también lo es la longitud de la curva. Integrando la expresión diferencial anterior, y viendo que
dq = 1/(r . r0 )
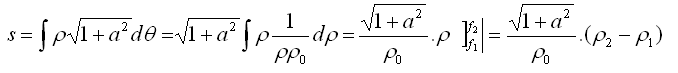
o sea la distancia entre dos 'frecuencias', depende únicamente de su diferencia, no de sus valores individuales.
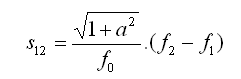
como afirmábamos:
La distancia sobre la curva es proporcional a la diferencia entre las frecuencias correspondientes.
Por lo tanto todos los harmónicos son equidistantes sobre esa curva, como ocurre en un espectro. de rayas. Esta similitud nos sugiere representar un espectro de ese tipo sobre la espiral: podemos usar un círculo tanto mayor o más oscuro sobre el punto de la espiral correspondiente a ese, o en perspectiva, levantar un segmento vertical cuya altura es proporcional a la amplitud de ese harmónico o a su logaritmo, en unidades de tipo decibelio.
Véala prolongada a tres dimensiones en forma de zigurat:

Se habla de esta espiral y la consonancia en EL MAPA de las VECINDADES entre NOTAS
Otras espirales para diferentes vecindades o consonancias
No es esta la única espiral posible. podemos asignar una vuelta no ya a la octava (separación entre los harmónicos 1 y 2), sino cualquiera de los demás intervalos, que quedarían así enfrentados y avecindados por esa particular colocación. Dispondremos así de espiral a la quinta, a la cuarta, a la tercera mayor, a la menor, etc. Se muestra en la figura la correspondiente a la 12ª. razón 3, con lo que se enfrentan los harmónicos en esa razón mutua: 3,9,27...; 4,12,36.. 2, 6, 18..., etc.
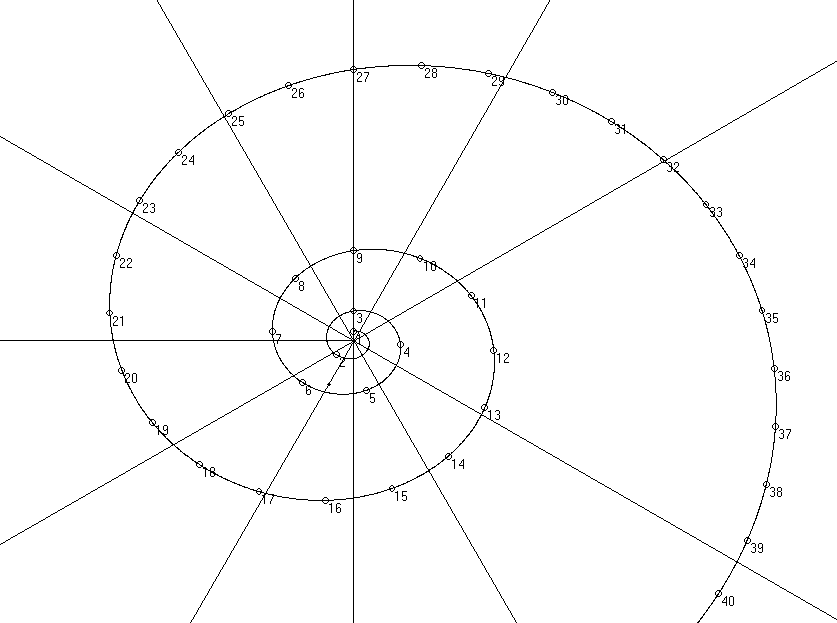
Se trata de una espiral como la anterior, pero algo desenrollada, como un muelle de reloj que estiramos y abrimos.
El juego de consonancias o vecindades es simultáneo, de modo que todas las espirales actúan imaginariamente, están presentes en un espacio de dimensión infinita.
Otra espiral: Lineal
0. Ecuación.
En este caso tanto el radio como el ángulo de las coordenadas polares de cada punto de la espiral, son proporcionales al intervalo con una cierta frecuencia determinada. Eligiendo la octava, que designamos por oc., asignamos asimismo cada una de ellas a una vuelta completa. De modo que el ángulo, en radianes, vale
q =2p ln( f / f0 ) / ln (2)
ya que para f / f0 =2, una octava, el ángulo vale en efecto, una vuelta, 2p radianes.
A su vez, el radio lo elegimos arbitrariamente también proporcional al intervalo logarítmico.
r =r0 ln( f / f0 ) / ln (2)
de modo que para la primera octava-vuelta, tenemos r =r0 el radio es igual a un radio inicial arbitrario.
Eliminando la variable intervalo entre ambas ecuaciones paramétricas, se obtiene la ecuación en coordenadas polares:
r =r0 . q
con el parámetro arbitrario r0 que depende de las unidades de dibujo. y que 'abre' más o menos la espiral.
La espiral obtenida no es ya logarítmica, y presenta volutas equidistantes al crecer el ángulo.
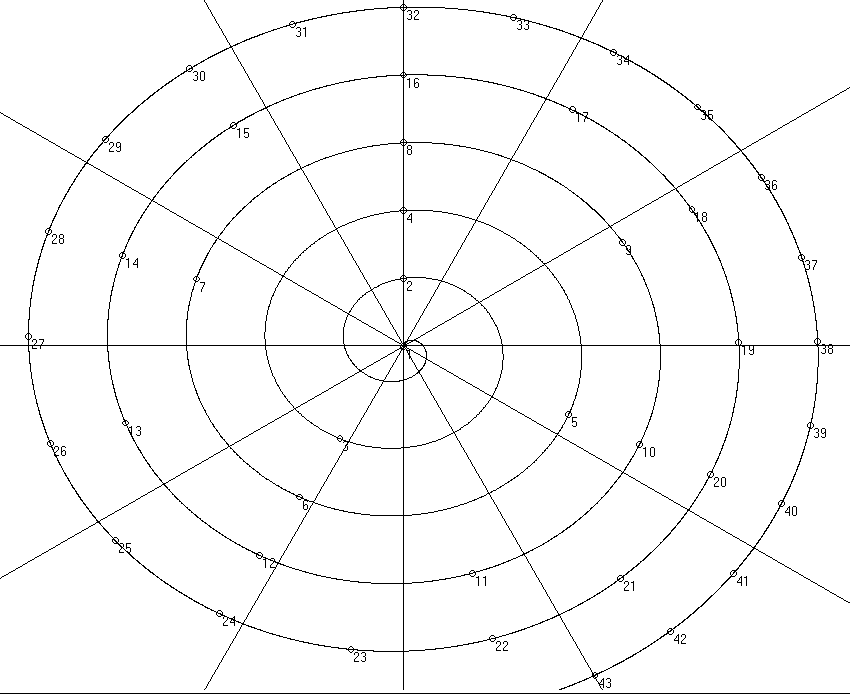
1. Según estas definiciones, radio y ángulo crecen proporcionalmente, ya que representan esencialmente el mismo parámetro: el intervalo con el fundamental. Pero es el ángulo el que resulta más informativo e intuitivo, ya que se visualiza bien la octava como una vuelta, y los semitonos temperados sobre uno de 12 radios igualmente espaciados en el círculo (pero no ya sobre la curva en este caso).
Longitud de la curva
El elemento de curva, cuya longitud es ds, forma, como hipotenusa, un triángulo rectángulo con dos catetos, el elemento de arco r dq y el crecimiento diferencial de radio, dr (véase figura anterior). lo que conduce a la expresión de la longitud del elemento de curva:
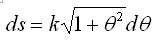
siendo k =r0 /2p
Integrando ese elemento entre dos puntos de ángulos q1 y q: obtenemos la longitud de la curva entre dos ángulos:
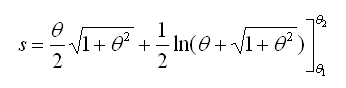
expresión más complicada que en la primera espiral.
Su derivada ds, demuestra que es una función ligeramente decreciente con el ángulo que converge hacia él cuando es grande, al perder entonces importancia el sumando 1 bajo la raíz. En cuanto a la frecuencia, en la figura vemos que por cada harmónico en una espira hay dos en la siguiente. Sólo que la curva es cada vez más plana de modo que la distancia sobre ella crece menos rápidamente que el doble.
En cambio encontramos la propiedad de que las vueltas o espiras están a igual distancia unas de otras. Todos los harmónicos múltiplos de 2, por ejemplo, distan lo mismo de sus vecinos en la serie. Se prueba fácilmente. Para dos frecuencias en proporción fija:
r2-r1 =r0 ln( f2 / f1 ) / ln (2)
expresión constante si el neperiano del cociente de las frecuencias lo es. De modo que para un intervalo constante, la distancia entre espiras, la diferencia de los radios, es constante. Así se aprecia en la figura. Esta distancia es, para cada tipo de curva igual. para las curvas de octavas, encontramos, justamente que esa distancia es precisamente r =r0 ln ( 2. f0 / f0 ) / ln (2) = r0 la distancia entre el origen y la primera octava.
La espiral inversa
Si prolongamos esta segunda espiral con las frecuencias e intervalos descendentes desde la frecuencia de partida, f0 , encontramos la rama homóloga de la ya vista, cuya ecuación es la misma:
r =r0 /2p . q
pero extendiéndola a valores de r y q negativos. Obviamente un valor negativo del primero corresponde a un sentido opuesto del vector sobre su dirección, de modo que al prolongar q hacia valores negativos, también lo hace r con lo que la expresión anterior es en efecto válida para esta otra rama, como adelantábamos.
La rama negativa, llamémosla así, comienza como su homóloga por un valor pequeño y crece con el ángulo. se desarrolla simétricamente a la otra respecto al eje horizontal (esto debido al comienzo del ángulos en el eje vertical y crecimiento de ángulos hacia la derecha, en el del reloj. Las octavas con la referencia aparecen ahora abajo (acordemente con el sentido descendente de los intervalos) .