Esta página está en construcción: perdonen los errores y temas inacabados.

This page is being developed: I am sorry for errors and unfinished subjects.

 ESCALA. Automatic Measurement of Oriental Scales.

 

 

ABSTRACT. Oriental (Arabic, Turkish, Persian, North Indian, Byzantine, Flamenco) music cannot  be adequately represented in the Western tempered scale, as is well known. The automatic measurement of oriental scales of maqamat and similar musical forms is a complex process, according to the complexity that these musical forms present. Pitch, Note, Interval, Scale, Consonance Structure and Maqam are stages of this analysis, assisted by correlative models of these aspects; we are far from tempered semitone scale recognition. The program ESCALA executes all those tasks on recorded or actual sounding music, by means of personal algorithms of pitch estimation and pattern recognition methods. ESCALA permits an accurate real‑time measurement of pitch shades, with a careful notation in 53‑degree/octave Hölder commas, in 72‑degree/octave commas, or in almost exact Cents. Moreover, ESCALA can find the main consonances to estimate the modal tonic, and its related hierarchy. musical examples of those kinds of music, and their scale evaluation, will be presented during our talk, and our original pitch estimate methods will also be discussed.

 

INTRODUCTION

 

The so-called Oriental Music in the West, employs a very rich and complex set of tones (pitches) and rhythms that are constitutive elements in this music; the tempering or rounding off those pitches impoverishes and converts it into tasteless stuff. The mastering of those shades of pitch, and their use in actual music (maqam, dastgah, raga), are a matter of time (a lifetime) which few persons, in the West or in the East, are disposed to or have the possibility of dedicating to it. However, only the person who does so, receives the richness of a Music which find its roots in the Past and blooms in the Present [1, 9, 16, 17, 23, 31].

 

Music comprehension and enjoyment is a question of playing, communicating, receiving sounds and hidden meanings; but, from the musicological point of view, it is also very important to know the theory of the system and language involved in the music of a particular culture. The  experts in the practice of this music (musicians, and some listeners) are able to pick up those shades of pitch, formerly described. But special conditions of listening and performance are needed, and no person can perceive all the shades in all the cultures: each listener always tries to understand a pitch as one of the elements of its own musical language (top of the list, the Western musicologist, who calls Do, Re, MI - c, d, e-,  notes with other function, meaning and  pitch).

 

We should not forget that in traditional music the tone, the note, is made by and for the finger, the vocal string and air pressure of the performer, much more than in the Western Music, where tone is fixed in the ear of musicians and listeners, as in many musical instruments (piano, organ, vibraphone, electronic instruments). As a conclusion, we can assume that Oriental Traditional Music is much more aware of pitch than Western.

 

The kind of music for which we intend our measuring tool to be useful, is primarily the cultured Oriental; in that wide concept we include: Arabic (A): Iraqi, Syrian, Egyptian; Turkish (T); Persian-Azeri (P); Andalusi-Mahghrebi (M); Byzantine (B); Oriental Christian (C): Armenian, Syrian, Maronite, Copt; Western Christian (G): Gregorian, Ambrosian, Roman, Beneventine; Indian (I): Pakistani, some Afghan; we include Spanish Flamenco or Cante Hondo (H) too; for a scale measurement alone we can work on any monodic music (Chinese, Japanese, Indochinese, Malayan, Javanese, etc.); and of course, all Folk (F) Music, which often sings free from the cultured framework. See [4-11, 14-23, 25-27, 29-30, 37, 39, 45-46, 48, 50].

 

To approach those various musical systems, a general code and a way to relate it to a specific music, are necessary, that is, a fine division of the octave, and a fine tool of measurement. This tool is valuable, not only to understand a particular kind of music, but also to know its tone system, establish its theory, and assist in its practice. This measurement must approach the perceived tone or pitch, rather than the fundamental frequency, a physical parameter not entirely proportional to it.

 

MUSICAL CODE AND NOTATION

 

We adopt a notation based on the division of the octave in 53 equal intervals; these intervals are called Hölder commas: they have therefore a size of 22.6 cents. With an error less that 1.2 cents, the major and minor Pythagorean and Natural (Zarlino) scales are represented by any of these 53 degrees; both scales will appear therefore with their usual names, c, d, e, (do, re, mi) etc. We take the Major Pythagorean as the basís of our notation [3, 7].

 

The deviations with respect to the Pythagorean Scale will be expressed by the usual symbols together with the deviations in commas, according to the following list:

 

                    commas         rising       lowering

                          1              +              ‑

                          2              *               =

                          5                                b

 

In this way we cover all the 53 degrees,  in the tone intervals ( i.e., do-re):

 

                        notes:          do    do+   do*    reb‑  reb   reb+   reb*  re=   re‑   re

                        commas:       0       1      2        3       4       5        6       7     8     9

 

and the semitones (i.e., mi-fa):

 

                        notes:        mi    mi+   fa=    fa‑     fa

                        commas:     0      1       2       3       4  

 

 the others 53 degrees being equally represented.

 

Thus the Zarlino Natural Scale will appear with a '-' comma in E, A, and B, and any other scale will be represented by a degree of the 53‑set with a maximum error of 12 cents (half a comma); however the actual error is usually much less because 'natural scales' mainly uses consonances, and these are well represented by the Hölder set. For instance,

             

            Arabic Mahur   would be:       C         D            E      F          G           A           B-      C

            Turkish Rast     would be:        C         D          E-      F          G           A           B-      C

            Egyptian Rast   would be:        C         D         E=       F          G           A         B=       C

            Egyptian Baiati would be:                   D        Eb*      F           G           A  Bb              C          D

            Persian Schur    would be:                   D      Eb+        F          G    Ab+     Bb              C          D

            Nahauand          would be:       C          D     Eb           F          G    Ab+               B      C

 

Note the fine pitch shades that this notation embodies, as in note E, for instance.

 

This notation is similar, but not identical, to those used by Danielou [6], and by Turkish Traditional Music [11, 30, 50]. The first, very accurate, is somewhat complex, because it take a Zarlino Scale as a basís, and employs major and minor tones, 4-comma flats, and a 1/4 interval, out of the comma status. The second adopts the Pythagorean Scale as its basís, but uses up till eight types of flats and sharps. We prefer our notation because we find it simple and intuitive, and also compatible with the usual western scale.

 

As a more accurate unity we keep the Cent, or hundredth of the tempered semitone; the immediate formula of direct and inverse transformation between frequency ratio and cent's interval of frequencies f1 and f2, is:

 

                       IC = 1731H ln (f1/f2)                f1 = f2 H e  ^{IC / 1731}

 

where 'ln' is the natural logarithm, 'e' is its base ( 2.71828 approx).

 

In relation with the tessitura, or octave notation, after comparing the French, American, and Piano criteria, we choose the most generalized today, assigning to 440 Hz. the name 'A' ('LA') and the Octave 3. Every other frequency will thus receive the corresponding name.

 

Other sets are used, the 72-set specially, introduced by Aristoxenus (IV Cent. B.C) [1], and favored also now at microtonal centers in Austria [13] and USA. It need some more symbols, but with no gain in accuracy to represent the consonant intervals. For non traditional music it is however useful, and also compatible with tempered scale.

 

PITCH ESTIMATION

 

The automatic measure of pitch is not an easy task, first because pitch itself is an ill-defined concept, half physical (fundamental frequency), half a product of our perception. We do not know for certain if our inner ear analyses sound in time domain or in frequency domain, and in each case what is the range of our analysis, nor are we sure of our psychological decision about the tone or pitch that we attribute to a particular sound. What we know is that, in natural pitch estimation, fundamental frequency, frequency range (tessitura), frequency content (timbre), duration and intensity of the sound influence our decision, the first parameter being the more important.

 

Therefore, a frequency measure should not be sufficient for our purpose, musical notation and recognition, and several physiological and psychological considerations must be taken into account: we need, in brief, a model of our perception of pitch. This model has been refined and implemented in our laboratory, for both speech and music signals. First we shall consider the difficult task of frequency estimation.

 

FREQUENCY ESTIMATION

 

After many years of research and development [33-38], we now have at our disposal a very efficient tool for pitch estimation, which we call ADA (for Auto-Dissimilitude Adaptativa). Briefly, for each short frame of the signal, we find out the delay for which the similarity between two short signal segments is greater, or minimal its dissimilarity. This delay correspond to the local period in the frame, if the dissimilarity is small enough (below a threshold); if not we will consider the frame as non-pitched. In mathematical language, the pitch P is the value of the delay τ for which the expression:

 

                                        2 f (t+τ) - f(t) 2

                    ADS(f) =  ────────────        is a minimum, below a threshold.

                                     2 f (t+τ) 2  -  2 f(t) 2    

 

where the norm 2 f(t) 2 of the function f is its power measure over a time window w(t), whose time support (interval) is proportional (equal in our case) to the delay τ. For digital (numerical) signals, this power measure is:

 

       2 f (t) 2  =  3  * f_i *   being the sum of the samples f_i extended from   i=t+τ/2  to  t+τ/2.

 

The function ADS (autodissimilarity), varies from 0 (perfect periodicity) to 1 (exact opposition), and equals .5 for random noisy signals. We have with it a measure of periodicity, setting the threshold in .3 for practical purposes (i.e., sequential analysis of musical or speech utterances). See [33-35] for more details.

 

Once we have a value for Pitch Period (in time units, milliseconds usually) we have also its inverse, Fundamental frequency, measured in Hertz, or Vibrations per second.

 

The values of pitch over a time interval can be stored to obtain a histogram of the pitches that have appeared during it. Some pitches will be more visited, showing the preference of the performer (or the instrument) for them: this histogram represents the scale, when the accumulated pitches show big peaks and valleys. If no peaks appear, we are then dealing with another kind of pitched sound, normally speech, where pitch varies continuously without strong preferences as in music.

 

An alternate algorithm for pitch estimation works in frequency domain [38]. We select a band of frequency that covers the range of one harmonic for each note, usually the first or fundamental. After an average of spectra of a music fragment is calculated, a specific panorama of mounts and valleys (a 'sierra') appears, as above, where the higher peaks represent the most important (frequent, intense) notes of the melody: this spectrum give us both the notes (the peak's situation), intervals (peak interdistances), and hierarchy (that is, relative pitch altitude).

 

The estimations of both methods are very similar, the difference being within some cents, but not equal. They could not be, as the first one take into account the contribution of ALL harmonics in the waveform, and therefore in the pitch period length; while the second only considers the situation of ONE harmonic, and in actual pitched sounds the harmonics are not exact multiples of the fundamental one.

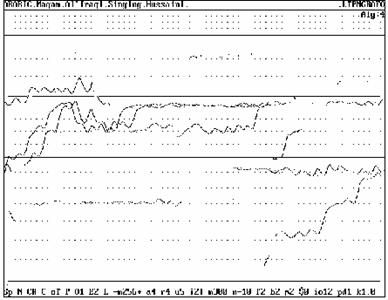
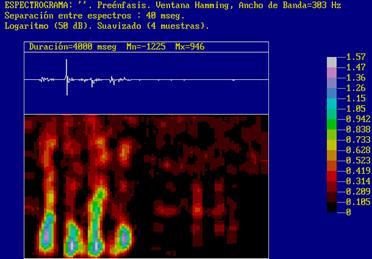
Fig.1.Singing Melody opening Maqam Al'Iraqui. First seconds.

 

Another important difference lies in the possibility, for the first method, to display the pitch as an instantaneous value for each moment, that is, for each frame of time selected by a window time of few milliseconds (i.e.,20); the second method means instead the value of pitch over greater duration (as .1 second). See this pitch evolution in Fig.1.

 

Other minor differences are due to the different quantization that digital process introduces in each domain: period lengths are calculated in sample units, while frequency appears in the spectrum as multiple of the inverse of frame time duration over which the frequency spectrum is calculated (by FFT algorithm). This means that the lower the measured period, the better the measurement of it in the first (time domain) method, and the worst the second one; inversely, for treble or high frequencies. These quantization effects have been much reduced by interpolation around the peak, which allow us to estimate finely its situation, i.e., the accurate frequency of the note represented by it. See more details in [38].

 

PERCEPTION MODEL.

 

We need now to introduce a perception model to estimate the impression that those frequencies are making in our ear and brain. Our Frequency-Pitch relation is related to the well-known Mel Scale, a mapping of physical measures into Pitch scale by an almost logarithmical function, with greater perceptual intervals in high and low sounds, a curve familiar to piano makers and tuners [28, 47, 49].

 

For practical purposes, that means that perceptual octaves correspond to a frequency ratio of 2:1 in the middle range (about 500 Hz.), but to more in the high and low parts of the keyboard, as much as a semitone more (ratio 2.05) in the extreme keys; and even more for sounds outside the range of piano (higher than 4000 Hz. and lower than 30 Hz, approx.).

 

We approximate this curve by a double potential function of the type

 

                        DCC ( f ) =  k1 .  | f - fc |   ^k2

 

where DCC is the decrement in cents that the physical frequency 'f' suffers in the ear, 'k1' the "control wheel", or parameter that controls the effect of "sharpening" the scale, with 0 for a tempered or plain 2:1-octave scale; 'k2' is the power exponent. These constants have been empirically determined by asking to musically educated subjects, to choose between scales played on an electronic keyboard tuned according these function and constants; after repeated tests, over all in the high frequencies, the parameters for the selected scale are recovered from the computer. The result depends on the timbre and on the subject, but as a general conclusion, we can assume variations of 2-3 cents for the central octaves, and of 5-7 cents for the neighboring ones. That is, the physical intervals must be greater than the theoretic ones to satisfy the tonal sense, at both sides of central A.

 

These variations are subsequently imposed on the measured intervals to be taken as the theoretic ones: thus a perfect octave in the 200-800 Hz area must measure about 1203 cents, and a perfect fifth, about 703, while towards the higher and lower frequencies, these measures should be 1207 and 705 approx.

 

MELODY REPRESENTATION.

 

The resulting pitch for each moment can be represented in the usual coordinates, time in abscissa and pitch in ordinates, with varying scopes for both variables. The drawing scales are linear for time and logarithmic for frequency as usual: pitch is already logarithmized, as it is measured in cents. The linear scale for time is enough to show pitch variation in time, but not to show relative values of note duration, which psychological estimation is also logarithmic, as the usual musical figure notation shows, in its double duration sequence:

 

w

h

q

e

r

 

The representation must also use some perceptive hypothesis: as we do not know for sure the temporal estimation of pitch in a glissando, the representation should afford some mechanism for it. Since pitch perception is much more fine and accurate the longer the steady frequency, we reject brief and sudden and little jumps of pitch: therefore we slightly smooth the melody curve. See Fig.1 again.

 

SCALE ESTIMATION.

 

The selection of main peaks will provide us with the frequencies candidates to scale components. But even this simple job suppose some previous knowledge or assumption about what is "main", or, moreover, what is a "peak"; the question is not a trivial one at all, as many sound signals, as speech [40], will not show clear peaks, and intermediate utterances, from poetry to Japanese theatre "Noh", will present preference zones but no definite peaks.

 

Therefore we will adopt an empirical way to choose note candidate to scales: peaks will be not too near,one to another, and not too numerous: their interval will have to be greater than a quartertone (50 cents), which will limit their number to 24 (for non-traditional microtonal scales -where everything is possible !-  that threshold can be reduced). To be a peak, the maximum height will be at least the double of its neighbouring valley values. A minimum range of peak heights can be also imposed: but this, only when the musical fragment is complete, or long enough to garantee the presence of all the notes.

 

Once all the main peaks are selected as notes, is is easy to name them according to the selected notation, which we introduced before. The expression for this conversion will be similar to the cent's; we only need to fix a frecuency reference f0, and the number of degrees in the octave, NDO (l2 is ln(2)):

 

                        INDEX(f) = int ( .5 + (NDO/l2) H ln (f/f0) )   mod  NDO    

 

This parameter will be 1 for octave assignement, 12 for tempered scale, 53 for Hölder commas and so on; furthermore, as the cycle of degrees will repeat each octave, we must take the modulus (rest of integer division) to have always a degree of the set for higher octaves: therefore, to assign octave 3 to 440 Hz, f0 must be 32.7 Hz. For the different sets, taken the exces rounding CEIL function for granted:

 

            OCTAVE(f)=(1/l2)Hln(f/32.7)                              PIANO(f)=(12/l2)Hln(f/32.7)mod 12

 

            HÖLDER(f)=(53/l2)Hln(f/32.7) mod 53             72-NOTE(f)=(72/l2)Hln(f/32.7) mod 72

 

For instance, the note of frequency f=546 Hz.will fall within octave 5, piano key inside the octave number 1 (begining in 0, this is c#,do#), the 3th Hölder degree , etc.

 

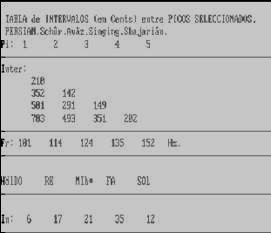
Fig.2. Interval Table for Dastgah Schûr. First Tetrachord.

SCALES and MUSIC.

 

We see a scale as a collection of notes, without any condition: therefore, there is no limitation about the pitch range, tessitura, interval sizes, and of course, temporal use of this scale in a melody. But it can be clearly understood that such scales are of little musical utility, with a possible exception of didactic purposes [3, 4, 12, 20, 23, 24]. Music uses only a limited part of those possible scales: Tradition, which includes perception laws and aesthetics, selection scales according the relations between their components. These relations are of two main kinds: Interval Distance and Sonance Distance.

 

Interval Distance is the usual interval measure, in semitones, commas or cents. Sonance distance is a less usual concept, however its universal presence in Music: Pairs of notes are more o less neighbor according what we call Consonance or Dissonance (let us group them into Sonance). Almost every natural (i.e., traditional) scale presents a strong parental structure that allows its musical use. Music can be seen as a regular oscillation between both extremes, tense and lax, and in the long view, as two great movements: Consonance-Dissonance-Consonance: modal tonic establishing, introduction of dissonances, with partial consonances, until we arrive to the end, when consonance imposes and relax the tension [41, 43, 44]. Let us develop this ideas into a Model, based on a set of hipothesis.         

 

PITCH, CONSONANCE and DISSONANCE.  Hypothesis on perception.

 

We confront the well‑known problem of consonance perception, setting the following hypothesis [43, 45]:

 

PH0. Perception extracts from a single periodic sound an impression called pitch; and from a combination of pitches an impression called dissonance or consonance. These are natural facts. Culture and Education modifies only its evaluation (can be found pleasant or not, according those factors and many others). Consonance has its processing in neural activity. Education can teach to recognize and use this perceptual phenomenon in a musical and artistic way, even rejecting it by avoiding easy (simpler) consonances.

 

PH1. We perceive an interval, and its consonance, as the simplest and nearest that belongs to the  musical code of the listener.  This means that, in a diatonic universe, we expect and force the notes we hear into belonging to this diatonic universe. If we shift to a chromatic one, we will have more codes, more categories to classify the sounds we hear. If we shift to a microtonal world we will perceive as meaningful and independent sound that were only varieties in a simpler universe. It does not mean that we accept as correct these sounds; only that we lack of a code for them, and therefore, they simply does not exist. It allows us to accept and recognize notes of mistuned instruments.

 

Another easy proof of that: a perfect temperate 5‑degree by octave scale will probably be perceived at first auditions as a pentatonic one. Our usual code, the 12‑tone temperate scale, forces these sounds to belong to it.

 

This effect allows us, for instance, the enharmonic, in which a unique pitch is perceived as forming consonances with two different groups of pitches; it is perceptively modified to fit into both groups.

 

PH2. Any interval has a perceptual SIZE that grows gradually. It has also a COLOUR, a character that changes by sudden steps, according to the prime integer numbers imbedded in the consonance. The names given in western music to the scale degrees (dominant, sensible) point to that colour. Oriental perception of these colours has traditionally been finer and more acute. For instance, Indian names for srhuti, shows this character. As we see in [6], in Indian classical music, the interval major third, when:

Of course this colour can be perceived and used only after appropriate training: but, as a manner of speaking, "it is there." By PH1, it can be simulated (until a certain point) by other neighbouring intervals, as in tempered scale, but losing however, we believe, an important part of its effect.

 

We can sum up saying that each number has a size and a colour: its size is its cardinal; its colour is its divisibility (structure). For a measure of sonance, see [12, 41, 45].

 

PH3. The longer we hear an interval, the better we perceive its size, its consonance and its colour. If we increase the density of degrees (number of notes in the octave, see M1,M2, next paragraph) our analyzing mechanism needs more time to discriminate between them, the same as any other mechanism, of Fourier type or otherwise. It means that, complying with PH1, we can understand quick pentatonic music but we would need microtonal music to be slow in order to discriminate between near degrees. If not we will probable hear something as clusters,  glissando, or loose at least the finer pitch shades.

 

This seems to be responsible for the fixed intervallic size of simple consonances and the variability of more complex ones (moving semitones, pien, variable degrees, etc).

 

PH4. Any judgement of consonance is made, in any moment, on the ensemble of the last sounds heard until this moment. It means that we attribute a measure of consonance to a cluster composed with the last sounds, even with those that have actually disappeared: they are held by the short-memory, and probably decay in importance as new sounds replace them. An important corollary is:

 

PH5. Any judgment of consonance must include the reference note (tonic or modal tonic) if the music suggest it. Consonance is acting during the entire performance: first, in stringed instruments, by the tuning of strings in simple consonances, usually fifths and fourths, and those strings will vibrate by resonance; secondly, during the actual playing, searching by ear the consonance by repeated essays around it in variable tuning instruments, as naï (flute) or 'ud (lute).

 

The choosing of determinate consonances (which usually means overlooking others) fixes the main notes of the mode; their hierarchies and structure are built in this way; read M4 in next paragraph.

 

STRUCTURED SCALE of a MAQAM.  A model of Modal Music

 

Our model of modal music, deduced from many automatic and natural analysis, is based on the following characteristics (several of them are common to other music). We believe this model to cover the musical systems of the areas named before. Let us see those characteristics:

 

M1. A limited range of pitches are used.

 

M2. They cover this range in a limited density; usually, from five to ten in an octave, mainly seven in many cultures.  This density can be calculated as MI, the mean value of interval: we find 240 cents for any pentatonic scale, 171 cents for a heptatonic and 100 cents (a semitone) for a dodecatonic.

 

M3. They are not usually perceptually equidistant, which means different interval sizes. We can measure this distribution by defining the Tension of a scale as the mean of differences of each interval with MI ( we could also weight each interval with the frequency of its use in actual music). We will find (without weighting) a tension value of 49 for a Pythagorean scale, 43 for major tempered and 34 for natural, which represent fairly well the subjective feeling.

 

M4. These pitches are selected between those which relates in simple consonances with one of them, at least some of them. These form, with the latter, that is called modal tonic, a skeletal structure of that music, as we said in PH5. Since they are simple, they must be octaves, fifths, thirds and its complement to the octave, quarts and sixths. As the main notes of the mode, they will appear insistently.  Secondary relations of consonance can be established with the elements of that structure, which is then organized as a tree with different levels and different hierarchy. A structure based on tetrachords (4:3) represents fairly well the central areas considered in our study (P,T,A), but is less clear in the extremes (I,M), where greater consonant intervals (fifths, sixths, even octaves) are directly used.

 

See in Fig 3 an example of the proposed  structure for the natural (Zarlino) scale on C, with its  consonant intervals up and the less consonant down; notes and interval in cents are indicated.

C                                            2:1                                           C'        ──────┬──────────────────     │                                     G     4:3              │       ├──┬────┼─────┬──────────────┤        5:4         E‑    6:5     │ 10:9  A‑   6:5       │      ├─┬──┼───┬───┼────┼───┬─────┤       │ 9:8    D 10:9  │16:15 F 9:8  │   │ 9:8  B‑ 16/15 │ ├───┼───┼──┼───┼───┼───┼─────┤            │        │       │    │        │       │        │     │       ┌───┬──┬───┬───┬───┬───────┐       cent  C__204___D_182__E‑_112_F__204__G__182__A‑_204__B‑_112_C'     Fig.3. A Structure for Natural Scale.

M5. This structure can be moved in frequency (tessitura) in a continuous way, according to particular conditions (instruments, voice, even mood) without changing its significance. There is no absolute pitch in that music. But after it is chosen in a performance, it does not change, it will sound during all the performance, always in the conscience of interpret and listeners (M,S,A,T,P,C,G,H,F), even actually sounded (I,P).

 

M6. The use of the notes is mainly melodic, moving by conjoint degrees, and covering a limited part of the total range. This part is usually a tetrachord or a pentachord, and is called genus. The interpreter present slowly and carefully these notes one after another, thus appearing gradually to the listener. With the fixed reference, each pitch acquires a very particular and strong function. The consonance is not the only expressive mean: the motif development, like a kind of prosody, is essential to the mode. But even melody makes use of (more subtle) consonances, which emerge out of the mutual relations between motif components.

 

M7. The structure described in M4. can be partially changed during the piece, making a kind of modulation (modal modulation) which modifies some of the consonances and their intervals, but not the modal tonic. It is like a part of the tree changing its branches and hierarchy, even some of the pitches in the maqam. This brings more than seven notes by octave, by grouping all the used in different moments of the performance. The melody can be seen as moving point on that structure, through branches (intervals) and nodes (notes); see  Fig.3.

 

M8. This ideal structure is realized (given reality in sound world) by making the consonances audible, which establish references, and the dissonances, which give instable moments which must be resolved: that makes the melody progress, and gives life to the music, in an alternative arsis‑thesis.

 

M9. This arsis‑thesis pair is repeated at all the levels. The highest is the whole melody and its end, which represent to the perceiver the return to the reference, felt as peace and resolution of dissonance problems proposed in the melody.

 

M10. The particular chosen consonances (intervals) determine a particular musical climate, a character, an emotive mood. This is called maqam (A,T), dastgah (P), raga (I), tub (M), mode (G), qolo (C), 'cante' (H), or any word according to the epoch, country and language (as tonos-tropos, in Old Greece). We think of that as a global harmonic timbre, specific of each maqam, which has an emotional effect on the audience (ethos).

 

M11. The most pure example of this melodic use is the so‑called taqsim (A), alap (I) istahbar (M) or muhtasari (P). In this improvised form (note the apparent paradox), the player constructs the maqam by establishing the scale degree by degree, in sections corresponding more o less to the genus range, and finishing in a partial consonance, the genus base note. In Far Eastern music (I), not easily structured in genera, consonance is equally working, providing tension and rest moments.

 

M12. Following traditional (tested effectivity!) rules, he develops the scales and intervals with almost prescribed notes of beginning and end for each section, and also prescribed order of each genus. But outside of these rules he will stay longer or not in a section according to his mood. The taqsim can take from half a minute to thirty.

Fig.4. Maqam Hussaini. Preference notes: Kirdan and Hussaini.

 

M13. A long duration of a section is achieved by delaying wisely the resolution which this section demands, i.e., rest on a partial consonance.

 

MAQAM ESTIMATION.

 

According to our model of maqam, its recognition from an analysis of its notes, main and secondary, is possible; however we do not use the temporal development of the melody, development which we know to be fundamental for maqam design.

 

As the interval sequence which represent a scale can be used in any tessitura, according the instrument, the voice, the country), is it clear that the absolute notes (as those of the piano) are of no relevance for our purpose: we must look for intervals, not for notes; Arabic rast will appear as C, D, Bb; Indian Sa will be C, C#, D, E, A, according the instrument, etc. The human (educated) ear is able to pick up the maqam type of a little fragment of music, for any instrument and tessitura: it is therefore clear that what we hear are not absolute notes (yet if we do, it will not be any consequence for maqam estimation), but consonance relations between the notes of the melody.

 

In our automatic system, therefore, we will first look for strong consonances, with some freedom in the tuning to accept little variations of style, on one hand, or minor errors of tuning, on the other. As we do not know, exactly, the interval ratios, we can not impose it on any music. As the octave is widely used in almost every scale, it will be not considered: only perfect fifth and forth, and also major and minor thirds will be looked for (in addition, for the frequency method, the second harmonic will appear at octave interval of fundamental)

 

The estimation of these consonances must necessarily be an approximate work, as no exact interval can appear, and what is more, we do not know what an exact interval is (see our perception model). A strong consonance will be, then, an interval which measure approximates of that which we consider a perfect interval: let us take exact numerical ratios as those references. If we have, for instance a fourth, ratio 4:3, very approximately 498 cents, we shall consider an actual interval as a fourth, when its measure is within a small range of error. However and again: "When and what is 'small'?" Our answer can be reached from our previous hypothesis: as the main consonances are easily perceived, they are rigid and admit a small range: let us say 10 cents. But lesser consonances, or dissonances, will admit a greater range, about 20-30 cents. Of course, when we approach these limits, we approach a bad or mistuned interpretation too.

 

For music which do not admit clear consonances (if it exist), as the well-cited Slendro and Pelog of the asían South-East, these consonance limitations must be relaxed, in order to know first their intervals, and after discover their "unity factor" other than consonance. But let us continue with consonance-patterned music.

Fig.5. Fix note playing: Persian Târ. Dastgah Schûr.

 

The notes which form the main consonances will be the main notes of the maqam; and probably the most intense in the histogram will be the modal tonic (the king) or the second one in importance (prime minister). These primary selections are needed because the same (or very similar) interval sequence can fit to different maqamat, changing only the references or main notes (Arabic Segah and Rast, Turkish Husseini, Ussak and Baiati, Turkish Ajam asíran and Chahargah, etc). See [5, 11, 21, 48, 50].

 

Once the consonances are found, we must select the probable genera scopes, that is, the chain of tethachords and pentachords forming octaves. Inside these scopes we will be able to detect the inner note intervals with the extreme notes, and from these intervals, to deduce the appropriate oriental name for it (see Appendix 1 for this attribution). The process is similar to the choosing a "nai" out of the set of seven, to play a melody: the player must recognize the intervals in the melody and contrast with those emitted by each flute. If besides and below a pentachord, we find the sequence tone-three quarter-three quarter inside a tetrachord, we should name the genus Rast, and make it begin in note rast (or naua) and finish in chahargah (or kirdan); and so on. We see how the estimation of the genus is paired with the name attribution to notes.

 

For irregular genera, that is, those whose extreme notes form not just intervals, as Saba or Huzzam, within different kinds of non consonant fourths, we must recognize before the main consonances, like the minor third which is present in both; and after see if the other notes fit into the pattern .

 

The process uses the information available in the set of selected tones, and crosses it with the stored models of maqamat; if two o more notes appear in the same zone (i.e. 'ayam and 'iraq, arabic B= and B=*), it will reinforce a classification: if 'ayam and 'iraq appear together with an important peak at rast, and dukah, segah,..., the maqam Rast will be selected. Furthermore, if the pitch of segah is high, i.e., E-, it will be considered Turkish or Iraqi, meanwhile if it is E=, or even E=*, an Egyptian origin will be suggested.

 

The more we want to recognize, the richer the model must be, taking in account finer shades of pitch and hierarchy: if a maqam going further in the taxonomic tree must be picked up, the necessary information should be stored in a way easy to recover and use in the recognition process. This storing of information is limited for the moment to the main maqamat of Arabic and Turkish music.

 

COMPUTER IMPLEMENTATION.

 

Fig.6.Speech Spectrum in the 0-5000 Hz. range.

ESCALA has been developed with the contribution of many researchers, as engineers,  programmers, and músicologists, in code optimized for speed and direct graphic control. Its use is easy and friendly, with a help menu for every job. musical and Speech signals can be recorded, visualized, stored, transformed and recovered as living sounds.

 

The model formerly described has been built in ESCALA to recognize the complex musical phenomena of Oriental, Natural or Traditional Music, following the perceptual model also described. For music not conforming with these natural models (i.e., with no consonance requirements), only the scale, or list of notes, is offered. Not only pitch information is available from ESCALA: Intensity and Timbre parameters are measurable too, for a better characterization of the sound source. See Fig.6. Spectrum of speech:"one, two, three, four".

 

ELECTRONIC TUNING.

 

Besides the measurements of scales, ESCALA is able to tune an electronic instrument, as keyboards, via MIDI interface. So, the user can reproduce the heard music on the keyboard, contrasting the effects of natural and measured tunings. The tuning itself is done by changing the pitch attributed to the note, permanently in the cases where it is possible, as for tuneable DX7-II and its family; or by means of Pitch Bend parameter, if not.

 

CONCLUSION

 

The work realized in ESCALA shows in a theoretical and practical way that Modal Music, in particular Middle East Maqamat are complex musical systems, far from easy tunes for entertainment. Escala measures on actual or recorded music the melody pattern and the subjacent scale, trying subsequently to recognize the particular maqam-scale used in the music.

 

The introduced Model illustrates too how the old principles of consonance, based in the human perceptual experience, and therefore timeless, oriented and continues to orient Music, Oriental and Western (even we do not show here the relationship between Harmony and Consonance, as we did for modal music). 

 

APPENDIX 1.

 

We present here our equivalence table between Oriental note names and its usual notation for the main systems, Arabic, Turkish and Farsi (Persian). Each kind of interval is represented as a segment with different slope, to show graphically its different perceptual meaning. The Western names are the used in the score writing, not their actual tuning, which we know to be variable. Despite the complication of the table, this is only a rough schema of the actual interval size. Notes as Segah and Íraq are higher or lower according, not only to their country origin, but also to the maqamat itself, because a different reference tone establishes different consonances and therefore different intervals and notes.

 

It subsist for us some doubts about the correct mutual position for some notes, i.e., Sabâ and Hijaz. Some notes remain also uncertain in its position, as the second degree in scale Hijaz, and fourth in scale Turkish Huzzam, where the theoretical 5-comma interval naua-hisar became in practice  6 or 7 comma. Moreover, as we know, degrees and intervals vary from country to country, even from region to region.

 

For all these reasons the table must be taken more as a reference chart that as a exact measure interval. The transliteration will not probably satisfy all the readers, because of its mixed linguistic origin; but at least it will be understood, we expect, by all.

─────────────────────────────────────────────────────────────────── FAR─TUR─ARA ─────────────────────────────────────────────────────────────────── Do  Re  Sol │ RAMAL TUTI.  .   O  Basic ARABIC‑TURKISH‑FARSI SYSTEM             │                                 INTERVALLIC STRUCTURE         Fa#+│ Sabâ                                   Javier Sánchez          Solb│ Jauáb Hijâz                                 LTPM,1993              │                                             Sib Do  Fa  │ MAHURAN . . . . . .   O  . .        11                │                                     O    9 La  Si  Mi  │ Busalîk          O                  A    O  8         Mi‑ │ BUZURG              O                    T  O    5         Mib+│ Ushshák.                O                     K  O  4         Mib │ Sünbüléh                   O                     S  O             │                                                     B Sol La  Re  │ MUKHAYYÂR             O                        O              │                                                         │                                           Represented             │ Shahnaz                         O           Intervals              │                                       Value in Commas FA  SOL DO  │ KIRDAN. . . . . . . . . .  O                                      │                         Si  │ Mâhûr                 O                           Si‑ │ AUJ                      O                               │              Mib Fa  Sib │ 'Ajam Hussáini                  O                               │  Re  Mi  La  │ HUSSAINI                   O                         La‑ │ Hisarek                       O         Lab+│ Hisár                             O          Lab │ Nim Hisár                            O                 │ . Do  Re  Sol │ NAUÂ.  . . . . . . . . . . . .  O  . . . . . . . .             │                           Fa#+│ Sabâ                                   O         Solb│ Hijâz                         O                     │               Sib Do  Fa  │ CHAHARGÂH  . . . . . . . . . . . .   O  .  . . .              │                     La  Si  Mi  │ BUSALIK                         O                         Mi‑ │ SEGÂH                              O                             │ Ushshak.                               O                 Lab Sib Mib │ Kurdî. Nihawând                           O              │                      Sol La  Re  │ DUGÂH                                O                             │                                    │                              Do# │ Zirgülé                                        O              │                      FA  SOL DO  │ RÂST . . . . . .  . . . . . . . . . . .   O . . . .             │ Mi Fa#+  Si │ Gawásht                              O              Si‑ │ 'IRAQ                                   O             │             Mib Fa  Sib │ AJAM 'USHAIRAN                                 O             │                     Re  Mi  La  │ 'USHAYRAN                                 O                   │                        │                          │                          │                                          Do  Re  Sol │ YAKAH . . .. . . . . . . . . . . . . . . . .   O   ───────────────────────────────────────────────────────────────────

 

BIBLIOGRAPHY

 

[ 1] BARKER,A.(ed)         Greek musical Writings,II:Harm&Acous.Theory      Univ.Pres.Cambridge.1989

[ 2] BENADE,A.H.            Fundamentals of musical Acoustics.                           Oxford, N.York,1976

[ 3] BLACKWOOD,E.      The Struct.of Recognizable Diatonic Scales               Princ.Pr. Princeton.1985

[ 4] DomCARDINE.          Semiología Gregoriana.                                                Abadia de Silos, 198.

[ 5] CHERKI, S.                Al‑Moustadraf dans le regles..                                     Rabat, 1972

[ 6] DANIELOU,A.            Traité de Musicologie Comparée.                               Hermann, Paris, 1959

[ 7] DURING,J.                  Le repertoire modele de la mus. iranienne: Radif.     Soroush, Teheran,1991

[ 8] ERLANGER,R.D'       La Musique Arabe. Vol.1‑6                                          Geuthner, Paris 49‑64

[ 9] GEVAERT,F.A.           Histoire&Théorie d.l.Musique d.l'Antiquité               G.Olms, Hildes 1965

[10] GUETTAT, M.            La Musique Clasíque du Maghreb.                               Sindbad, Paris, 1980

[11] HAKKI,I,Ö.                Türk Mûsikîsi Nazariyati ve Usûlleri.                          Ötüken Ne, Istanbul,1984

[12] HELMHOLTZ,H.      On the Sensation of Tone.                                             Dover, N.York,1954

[13] HERF,F.R(com)        Mikrotöne I,II                                                                Helbling , Innsbruck.1985,1987

[14] JARGY,Simon           La Musique Arabe (Que sais je?)                                 P.U.F., Paris, 1971

[15] JEANNETEAU,J.       Los Modos Gregorianos                                               Abadía de Silos, 1985

[16] Al‑KATIB                  Kitab Kamal Adab Al‑Gina     Siria,s.IX

  (SHILOAH,A.)                 La Perfection des Conn.Music.                                  Geuthner, Paris, 1972

[17] Al‑Fasí                       Kitab Al Jumu Fi Al Musiqi ...

  (FARMER,H.G.)              An Old Moorish Lute Tutor                                          Civil Pr. Glasgo,1933

[18] Coll.Int.du C.N.R.S    Acoustique musicale(Marseille,1958)                       C.N.R.S, Paris 1959

[19] KASZIM, A                Terminology of Oriental Music                                   AlJamhuri, Bagdad,1964

[20] KARAS,S.                  Harmonika:Des consonances par moy.harmoniq.      Manoutios. Athène.1989

[21] KARADENIZ, E.       Turk Mûsikîsinin Nazariye...                                         T.Bank.Y Ankara,1965

[22] LACHMANN,R.        Musica de Oriente.                                                        Labor, Barcel.1931

[23] LEON TELLO,F.       Estudios de Historia de la Teoría musical.                 C.S.I.C. Madrid.1962

[24] LLOYD,H.B               Intervals, Scales and Temperament.                             S.Martin N.York,1963

[25] MALM, W.P.             Culturas Mus.Pacifico,Cercano Oriente&asía           Alianza, Madrid,1985

[26] MAHDI,Sal.El            La Musique Arabe.                                                        Leduc, Paris, 1972

[27] ÖZCAN, I.H.              Türk Mûsikîsi Nazariyati ve Usulleri.                          Ötüken, Istamb.1984

[28] ROEDERER,J.G.       Intr.Physics and Psychoacoustics of Music.               Springer, N.York,1979

[29] Al‑RAJAB,H              Al Maqam Al‑Iraqui.                                                      Al-Ma'arif, Bagdad,1961

[30] REINHART,K&U.     Turquie. Les Traditions musicales.                              Buchet/Ch.Paris, 1969

[31] SACHS,K.                   La Musica en la Antiguedad.                                         Labor. Barcelona.1934

[32] SACHS,K.                   Musicología Comparada.                                              Eudeba, B.Aires,1966

[33] SÁNCHEZ,F.J.           Dissimilarity and Aperiodicity Functions. Temporal

                                                processing  of Quasíperiodic Signals                      9.ICA Cong., Madrid,1977.

[34] SÁNCHEZ,F.J.:         Application of Dissimilarity and Aperiodicity Functions

                                                to Pitch Extraction and Voiced‑Unvoiced Decision.  9.ICA Cong., Madrid,1977.

[35] Sánchez,F.J.           Tratamiento Señales Pseudoperiódicas.Ph.D.            Un.Polit. Madrid,1979

[36] Sánchez,F.J.&all   S.E.T.S.v.1B. Manual Referencia.Manual Usuario     LTPM, C.S.I.C., Madrid, 1990.

[37] Sánchez,F.J.           La Musica Culta Arabe Oriental                                   Coop.Univ.Madrid,1985

[38] Sánchez,F.J            Analisis de interv.y escalas modales.                           Rev.Esp.Mus.Madrid,1989

[39] Sánchez,F.J            The 8/7 interval in arab and related music.                  Mus.Sympos. Bagdad.1989

[40] Sánchez,F.J .          Interválica musical subyacente en la prosodia.           Sym.Ling.Log. Madrid.1989

[41] Sánchez,F.J.           Acústica musical II:Intervalos&Consonancia .           U.A.M. Madrid,1989

[42] Sánchez,F.J.           Curso Acústica musical III: El Motivo.                       U.A.M. Madrid,1990

[43] Sánchez,F.J            Number as Music Builder: Sonance.                           Symp.Mús. Inform. Delfos,1992

[44] Sánchez,F.J.           Acústica musical V: Ritmo,Motivo,Sonan.Comp.      U.A.M.Madrid,1993

[45] Sánchez,F.J.           Beyond 12‑interval temperament in Arab Mus.                Musiked.Nymphe.Munchen,1993

[46] STRANGEWAYS.F The Music of Hindostan                                                 Orie.Rep. Delhi 1975

[47] TOBIAS,J.V.           Foundations of Modern Auditory Theory                   Ac.Pres N.York,1970

[48] TOUMA,H.H.         La Musique Arabe                                                          Buch/Chat.Paris, 1977

[49] WINCKEL,F.          Music, Sound and Sensation                                         Dover, N.York 1967

[50] YEKTA BEY,R.        Türk Mûsikîsi Nazariyati ve Usûlleri.                        Pan Y. Istanbul,1986

 

---

Vuelta al Principio   Última actualización: Thursday, 21 de February de 2013   Visitantes: