Proporción de oro

Esta página está en construcción: perdonen los errores y temas inacabados.

This page is being developed: I am sorry for errors and unfinished subjects.

Proporción de oro, golden proportion, regla de oro, media y extrema razón...

De mucho juego y tradición a lo largo de la historia de las matemáticas y del pensamiento en general. Vamos a buscarlas una a una, al modo ingenuo que caracteriza muchas de estas páginas.

La proporción no es racional, no se produce comparando (o dividiendo) dos enteros, sino real, un número con infinitos decimales, más o menos igual a

F = .618...

y exactamente se define como

	√5 - 1
F =	--------
	2

y emerge en numerosas situaciones, como decíamos.

Este número posee muchas propiedades. Una de las más interesantes es su perpetuación en sus potencias. En efecto el cuadrado de F, su producto por sí mismo (por supuesto, pero déjenme ir paso a paso), lo que da:

(√5 - 1) (√5 - 1) / 2.2 = (5+1-2√5 ) / 4 = (4 + (2 -2√5) ) / 4 = 1- (√5 - 1) / 2 = 1 - F.

De modo que, curiosamente:

F² = 1 - F

Continuando con el cubo:

F³ = F ( 1 - F ) = F - F² = 2F - 1

y así, sucesivamente, encontramos una sucesión de potencias:

Potencias de F	Coeficientes de		Valor	Sucesión de Fibonacci
Potencias de F	1	F	Valor	Sucesión de Fibonacci
0	1	0	1.000.	0
1	0	1	.618...	1
2	1	-1	.382...	1
3	-1	2	.236...	2
4	2	-3	.146...	3
5	-3	5	.090...	5
6	5	-8	.055...	8
7	-8	13	.034...	13
8	13	-21	.021...	21
9	...	....	....	...

y vamos obteniendo en los coeficientes, en ambos, una sucesión con signos alternando entre positivo y negativo. Con valores positivos resulta la llamada sucesión de Fibonacci, cuya propiedad principal, su manera de generación, es la de que cada término es la suma de los dos precedentes. y siendo la serie de coeficientes de F la misma serie que la de 1, pero retrasada un puesto. Esa es la que adoptamos.

De hecho podemos tomar la ecuación F² = 1 -F como definición de F, y de ahí encontramos su valor, el citado al principio.

Las potencias de F pueden considerarse como vectores en un espacio de dos dimensiones; cualquiera de ellos resulta como una combinación lineal de los dos vectores de base, que son 1 y F . Se trata de un Espacio Vectorial (similar en su comportamiento al de los números complejos, combinación lineal de 1 e i), ya que posee sus propiedades.

Serie inversa

Si calculamos las potencias inversas de F, las sorpresas continúan: multiplicando en el denominador la suma por diferencia --diferencia de cuadrados--- obtenemos sucesivamente:

	2	2 ( √5 + 1)	√5 + 1
F^-1 = 1 / F =	-------- =	------------- =	--------- =	1 +F
	√5 - 1	5 -1	2

bella expresión que nos permite hallar las potencias sucesivas de exponente negativo:

F^-2 = (1 +F ) ²= 1 +F ²+2F = 1 + 1 - F + 2F = 2 + F

y, sucesivamente encontramos demás potencias negativas; representándolas en el cuadro como antes, queda:

Potencias de F	Coeficientes de		Valor	Sucesión de Fibonacci
Potencias de F	1	F	Valor	Sucesión de Fibonacci
...	...	....	....	..
-10	89	55	122.992...	0
-9	55	34	76.013..	55
-8	34	21	46.979..	34
-7	21	13	29.034..	21
-6	13	8	17.944..	13
-5	8	5	11.090..	5
-4	5	3	6.854...	3
-3	3	2	4.236...	2
-2	2	1	2.618...	1
-1	1	1	1.618....	1
0	1	0	1.000...	--
1	0	1	.618...	1
2	1	-1	.382...	1
3	-1	2	.236...	2
4	2	-3	.146...	3
5	-3	5	.090...	5
6	5	-8	.055...	8
7	-8	13	.034...	13
8	13	-21	.021...	21
9	...	....	....	...
10
...	...	...	...	...

donde volvemos a encontrar la serie de Fibonacci, ya siempre con términos positivos, y siendo la serie de coeficientes de F la misma serie que la de 1, pero retrasada un puesto. Esa es la que colocamos en la última columna por simetría con las potencias positivas. Se ve que este valor, 1.618 es más cómodo que el otro, porque genera la misma serie en ambos coeficientes, como antes pero ahora con términos positivos.

Si aproximamos el valor de este número mediante quebrados (como se indica en Simplificacion aproximada de frecciones), encontramos los sucesivos cocientes de términos contiguos de Fibonacci.

Aprox 1.618033988749895 Frac: 3.23606797749979 / 2 Expocal= 2

‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑ ‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑

fracc.aprox error: abso rel(*den^expo) cents(abs) cent/den

2 1 3.82E‑01 0.382 366.860 366.860

5 3 4.86E‑02 0.438 51.261 17.087

13 8 6.97E‑03 0.446 7.436 0.930

34 21 1.01E‑03 0.447 1.084 0.052

89 55 1.48E‑04 0.447 0.158 0.003

233 144 2.16E‑05 0.447 0.023 0.000

610 377 3.15E‑06 0.447 0.003 0.000

1597 987 4.59E‑07 0.447 0.000 0.000

987 610 1.20E‑06 0.447 ‑0.001 ‑0.000

377 233 8.24E‑06 0.447 ‑0.009 ‑0.000

Aproximación del número de oreo mediante fracciones (quebrados).

No es de extrañar porque en la serie si vemos que las potencias sucesivas de este número que aparecen en el cuadro anterior, cuyo cociente, claro, es F, contienen coeficientes de F iguales a parejas contiguas de F, precisamente -- . No aparecen todos porque se ordenan por calidad, es decir, enteros pequeños en relación a la aproximación obtenida. Por ejemplo 13/8 aproxima ya un 6 por mil.

Trigonometría

Como valor trigonométrico corresponde a los ángulos:

F
razón seno coseno tangente

.618...

.arco º º º

Geometría.

La geometría es el dominio idóneo para esta proporción. Ya hemos encontrado este número en las redes de cinco o diez direcciones en la lacería islámica, en concreto en Diseño de redes de 10.

Primero su construcción, sencilla

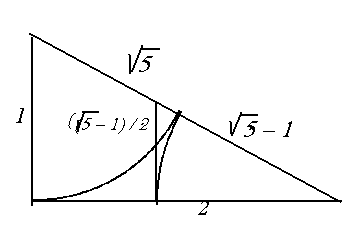
Otra aplicación de este número es el aprecio que despierta en un rectángulo de lados proporcionales a F: contémplelo. Se dice que es perfecto y harmónico como tamaños relativos en cuadros y marcos. Valore esa impresión en el rectángulo amarillo (el blanco es el 'marco' o passe-partout). Pero recuerde ajustar primero su pantalla para que las dimensiones vertical y horizontal midan lo que anuncian que miden.

Dibujando la estrella regular de cinco puntas, también llamada pentáculo en los tratados esotéricos, encontramos F en la proporción entre los segmentos que genera cada lado de la estrella en los demás. Se prueba recordando que en cualquiera de los triángulos isósceles que aparecen en la figura, por ejemplo, en cada una de las cinco puntas, los ángulos son respectivamente, p/5, 2p/5, p/5. Por el 'teorema del seno' (los lados opuestos a cada ángulo son proporcionales a los senos respectivos ) los lados son proporcionales a sen(p/5) / sen (2p/5) = 0.618 = F. Y por tanto los tres segmentos en que quedan divididos los lados de la estrella, son proporcionales a 1, F, 1.

Podemos dibujar nuevas estrellas trazando paralelas a los lados de la estrella que pasen por los vértices del pentágono central. Y nuevas en ellas con igual criterio. Cada lado se eriza con estrellas cada vez menores, todas compartiendo los picos de la original. Las distancias entre paralelas van disminuyendo en la proporción dorada. Y lo mismo las longitudes de lados homólogos en la sucesión de estrellas que acabamos de generar. Cada estrella tiene todas sus distancias .618 veces menores que la precedente más grande. Y a su vez, cada una es 1.618 veces más grande, pudiéndose prolongar la generación hacia tamaños mayores: infinitos en lo pequeño, infinitos en lo grande.

Como arriba, abajo, según el Kybalyon.

Es curioso que aparezca la raíz de 5 en figuras de pentágonos normales y estrellados, pero no sabemos si tiene un significado especial o es una coincidencia numérica. Lo pensaremos a ver. Para ello intentaremos --palo de ciego-- ver si aparece la raíz de 7 en la lacería de 7; e intentaremos probar que se encuentran unas series de potencias de comportamiento similar al encontrado para el 5, nuestro número F.

Otras ocurrencias

También dicen que aparece en las longitudes relativas de las partes de una sonata, por ejemplo en la exposición y recapitulación (1 a .618).

Como intervalo musical es disonante, mide unos 7 semitonos y medio, y está comprendido entre las sextas mayor (5/3) y menor (8/5), aproximaciones vistas antes.

Se ve que la secuencia de Fibonacci, nos ofrece los principales intervalos en la música:

1:1, unísono. 2:1, octava. 3:2, quinta.. 5:3, sexta mayor, 8:5, sexta menor, 13: 8...

cuyos complementos en la octava nos proporcionan, la cuarta, las terceras mayores y menores....

Generalizaciones

Una es usar otras raíces, por ejemplo la de 17. Nos inventamos el símbolo, aunque ambos estarán probablemente ya inventados. Así obtenemos El número q, proporción de plata.