 |
Esta página está en construcción: perdonen los errores, repeticiones y temas inacabados.
This page is being developed: I am sorry for errors, duplications and unfinished subjects.
LACEWORK ANALYSIS:
THREE TILE WORK PANELS FROM ISFAHAN
ABSTRACT: Islamic, Pattern, Geometrical Decoration.
Archeological and artistic analysis of Islamic patterns needs the prior understanding of their geometrical design and properties: otherwise only fake patterns are obtained, and thus beautiful decorative designs are lost to the comprehension of scholars and admirers. Three tile work patterns belonging to the Friday Mosque of Isfahan are here analyzed and drawn by means of the graphical design package PU18. The original pattern in the photographic images must be first improved and its minimal shape found, i.e., the shape that reconstructs the whole figure by translations, gyrations and symmetries. A basic step is to find the net order over which the lacework is woven, that is, the number of different directions in the plane appearing in the figure. The form is thus reconstructed for further repairing or reproduction.
INTRODUCTION
In a previous paper [Sánchez,93] a model of Islamic rectilinear patterns derived from the observation of many figures of this kind was presented. It consisted of a set of rules that every actual pattern seems to comply with. The model was embedded in a computer package that provides these rules for the designer, allowing the economic coding of each pattern. Several figures edited and drawn with this package were also presented, in order to assess visually the validity of this model.
We take now a step further in the analysis of more complex examples of these designs, found in three Persian tilework panels which, while following the model (this is proved by the possibility of drawing them with the program) slightly change their parameters either to simplify the weaving of the tilework or to deceive the eye in a ingenious design. The present paper continues thus the line followed in the previous article, extending the understanding of this complex and beautiful art.
TECHNIQUE of ANALYSIS
To reach a acceptable enough model of an actual graphic - called, from now on, the original -, two approaches are necessary: the principal one is to understand the geometric regular properties of the lattice over which the Rige is built, from choosing some of the segments that appear in the lattice. The second one, of a secondary nature, is to superpose both figures to visually assess their similarity. The necessity of the first method is absolute: it is virtually impossible to make two figures exactly coincide when one or both of them are the reproduction of a natural object; these figures are never perfectly regular; moreover, the process of obtaining the image (photograph, print, photocopy, video, scan) introduces its own deformation, some of then natural, like perspective angles and light; some of them belonging to the technique used: resolution or grain, film or tape quality, noise, etc.
Therefore a theoretical model is essential to overcome these difficulties. On the other hand, the mental and visual comprehension of a figure is always required: the observer makes some rearranging, some hierarchical ordering and selection, without which no visual perception is possible. In our case a regular geometric model is necessary, both to understand the image and to draw it.
ARTISAN REFERENCES.
Of course, artisans uses templates and easy references, rather than theoretical calculus in geometrical and proportion calculation. Hence, the artisan includes, under the aspect of ornaments or designs, those references which guide him or her in tracing sloped straights and figure proportion. In tile work 1 we can see those references in the form of small roses and diamonds, which divide the side of this square pattern in 12 equal (or almost) parts, and afterwards 11 are taken as side measure of the square.
With this artifice the main angles can be found approximately: those belonging to 8-lattice are easy from the sides and diagonals of the square. The specific angles of 16-lattice, though not so easily, can still be obtained from those simple references in the periphery. PI/8 <> 22.5º is found as that with a tangent of 5/10 units, whose exact value is 24.44º; and all the others are similarly found. This construction rule produces non equal pi/8 angles, in the succession fron 0º: 24.44º, 20.54º, 24.44º, 20.54º, and so on.
These artisan rules, although not exact, preserve the shape from generation to generation, sufficiently to recognize the abstract shape represented in the tile work.
THEORETICAL ASSUMPTIONS.
The model realization of an original Rige is based on several assumptions, which narrow the infinite possibilities of parameters values. In the case of Rige figures, these premises are expressed in [Sánchez,1993;1995]. Let us summarize them again, with special attention to our objective: the analysis of an actual Rige:
0. The figure belongs to a plane. Riges are two dimensional figures.
1. Only straight segments appear in the model. Curves are considered as ornamenting or filling material.
2. All the segments are parallel to a finite number, usually small, of directions in the plane.
3. Figures can be considered as embroided in a lattice of infinite straights, like carpet web and weft.
4. The lattice produces polygons, plane portions limited by segments. The figure uses some of them. The simplest (with no segments inside) are called the Elementary Elements, EE
5. The angle between every pair of these directions is an integer divider of the whole circle. This integer is the lattice index.
6. The distance between any pair of parallel segments is an integer linear combination of basic distances.
7. The number of these basic distances is small, usually 2, for simple lattices ( small N ).
8. The ratio between these basic distances is related to N.
9. Most figures can be considered as composed of repetitions by translation of a part (usually square) of them, which is called their Translation Element, TE.
10. Most TE can be considered as composed of the repetition, either by symmetries and rotations, or by pure rotation, of a smaller part of them, which is called their Generative Element, GE.
11. The GE is the smallest part of the whole figure that can generate it. This is the only part that is coded, by means of basic angles and distances.
These basic assumptions conform a General Model of Rige figures, that allow us to interpret them by means of it, simplifying the choices: an angle will be one of the multiples of 2.PI/N, but not an intermediate value; a distance will be a particular linear combination of the basic distances, but only with integer coefficients.
 |
An important value of this general Rige model is that of the preservation of its shape throughout time: without it, the copying of a Rige by means of the secondary approach, trial and error, will bring a gradual degradation of this shape, loosing its beauty and sense, becoming a fake without internal coherence, and disappearing, like a degenerated species, through imitation and restoration. Some of these unfortunate cases can be seen in reproductions past their historic moment. These "modern" fakes are however sometimes as old as the seventeenth century.
REDUNDANCY and PARSIMONY
In Information Theory, Redundancy is used as a way to built robust messages, that is, messages that go through the transmission line and can be recovered afterwards, even in the presence of noise. The redundancy consists in repeating some information (codes) in the message; in this way, an eventual degradation of one of its repetition would not imply the loss of it, since the same information can be recovered from another one.
In the same way, a Rige must have redundancy to make its shape robust against noise, this being, in our case, the physical and human transformation that the form suffers through the time (centuries or millennia). If there is a meaning in the Rige (and we are sure this is the case indeed), this meaning will be protected by a robust (redundant) shape. Redundancy consists, in our case, of symmetries, similitude and equalities, coincident points and straights. This lead us to an economy of constructible elements, or better said, to parsimony, the old (but eternal) concept closely related to style, elegance, beauty. We thus arrive at one of the ways that Tradition conveys messages, meanings to posterity: designs with an in-built protection, that is, no degradable forms. These considerations give us a new rule:
 |
12. Lattices and forms will be as simple and economical as possible, reducing the number of different elements ( i.e. not reducible to others by geometrical transformations) to a minimum.
ILLUSION and DECEIT
Another characteristic of Rige Art is forcing slightly, up to certain point, the exact proportions and angles to deceive the observer into making visual interpretations belonging to another geometric world: we refer to metabolê, the visual correlated element of musical modulation, as we saw in [Sánchez, 93]. But we especially refer to the enharmonic metabolê, by which we understand the kind that is not evident, the metabolê that fakes another one. In this case the eye, like the musical ear, attributes a double belonging to a segment, which can be understood as fitting it into regular patterns, which belong in turn, to two ( or more ) lattices with close but slightly different angles or distances. This adds another rule, somewhat opposed to the former one:
13. A segment can be slightly slanted, bent or displaced to comply with several lattices.
THE ORIGINAL FIGURES.
We have chosen photos of three tilework panels in the Southern Eivan (porch) of the Masjomeh (Mosque) in Isfahan (Iran).
FIRST LACEWORK
 |
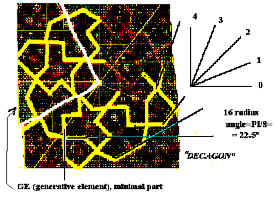 |
Fig.1 corresponds to a photo of a panel taken from a point of view below and leftwards of the perpendicular to the tilework plane in the pattern center. Its aspect is therefore rhomboid. The figure was first straightened, approaching it to a square as much as possible.
Let us fix out attention on the elementary elements (EE) shapes and numbers. In the inner square we found only 6 EE, with shapes reminiscent of decagons, arrow points, octagons, jellyfishes, pentagons and butterflies (d, a, o, j, p, b). If we count parts of them as different, the amount of EE is now 9 (the former plus the half arrow -ha- and the half and quarter decagons - hd, qd - ). Counting the number of actual EE in the whole square we find: 4 x (o + 4 x (j+b+p) + 4 x (qd+ha+hd+ha) + 4a +d = 73; and counting the number of complete or whole EE, we find: 4 x (o+ 4 x (j+b+p) + (qd-qd-qd-qd) + 2 x (hd-hd)+ 4 x (ha-ha) + 4a +d = 64. By using the abjad coding method, both totals sum up 10 (7+3 and 6+4), which decoded similarly again, gives 1, the symbol of Unity. Was this the purpose of the maker? We do not know, but still all these meanings are there.
 |
 |
| Fig.5.16-lattice vs 10-lattice patterns | Fig.6. Superposition of both. |
GE: Since we recognize easily two central perpendicular symmetry axes, parallel to the sides, we will center our attention on one of the four quarters (fig.2). We observe in this quarter further repetitions: a minimal part is repeated by turning it four times, at square angles, but without axial symmetry, in a gamma cross shape. We cannot find any other, nevertheless we do recognize an almost symmetry in that fragment, because the asymmetrical pentagon prevents it. We have thus the generative element of our Rige; and only the coding is left.
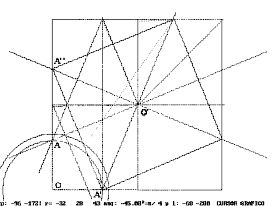
For that, let us find the lattice order. In fig 3, all the segments slopes were observed and grouped into a minimal set of main directions, which were counted up to 16 radii, almost regularly spaced, with some disturbance in the center, corners and sides centers, where clear decagons appear. We find, then, a striking contradiction between the first impression, a 10-lattice (decagon, as the Rige was originally called) and the slope grouping, that suggest a 16-lattice. This surprising fact implies a hidden complexity that we are going to try to uncover and elicit.
In fig.4 we see how point A is determined by straight O'A, of slope 22.5º passing by O', the quarter center. This provides us its with its symmetrical A', A''. The symmetry axes OA, OA', OA'' place the figure on the quarter, and the end of OA becomes an actual segment of the central decagon. In fact the angles are slightly different, as fig.5 shows in the left part.
 |
We can now describe and code the complete pattern (except the decagon disturbances formerly commented on) as:
Form Analysis:Four quarters with two mirror symmetry axes. Inside each quarter:PI/8 gyrated 16-order nets. Four quarters in swastika shape.Minimal shape:fragment in Fig.2
This description shows a particularity not yet included in our model: we have a GE circularly repeated inside of each quarter; and this quarter is circularly repeated in turn to form the whole pattern. We have, therefore a GE inside another wider GE. In this way the analysis of actual patterns impose the development of the model, to cope with new requirements.
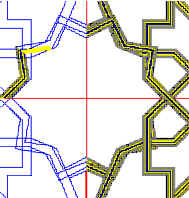
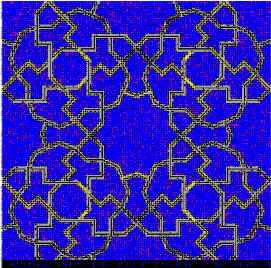
After coding and drawing the quarter we superpose both the original and coded pattern to assess their similarity and differences (Fig.6). The complete square con be seen in fig.7, which presents a final solution using 16-lattice only; the decagons can be seen as approximations with this lattice.
This is not the only solution of our problem. Several others have been developed, some of them including regular decagons, but they have not been shown here for limitation of space
SECOND FIGURE
The second pattern is presented in fig. 2-1. It is a rather simple one, with the particularity of having a 6-lattice limited by a 4-lattice Generative Element. The symmetry is rotational, giving a swastika look to the pattern. The space that surrounds the four main EE is included in the geometrical figure, as fig. 2-2- shows: the main lines, of 30º and 60º slopes, pass by important points in the lattice, as A, B; they limit the central and peripheral elements. The little roses form a beautiful background in colour and shapes, but also give references for the maker, marking directions, sides and vertices of the EE.
The centre shows the sacred names of Allah, Mohammed and 'Ali in kufic characters. There are only 5 EE. In fig. 2-3 is presented a reconstruction of the original pattern; no attempt has been made to reproduce the original colors nor the roses reference, only a general outlook is reproduced there.
 |
|
THIRD FIGURE
The third figure corresponds to another tilework panel from
the same origin. Its main characteristic is the presence of two Riges in it:
one, fine as a web, acts as a background for the second, in the foreground,
which is bigger and simpler. Let us begin with the latter, because the first one
is partially hidden by the second.
because the first one
is partially hidden by the second.
Rige in the Foreground.
Fig.3-3. Lattice, EG and TE of background in tilework 3.
We find 25 EE, in 3 shapes: octagons, butterfly tie and 4 pointed stars; this number becomes 6 if half ties and half and quarter octagons are considered. The number of EE is reduced to 16 if we count only complete figures. As in tilework 1, the sums of its ciphers 2+5=1+6=7, a number with many traditional meanings.
Lattice Angles: We observe a lattice of 8 radii, so 4 different directions, beginning in PI/8 < > 22.5º in steps of 45º.
GE is inside triangle OAB (Fig. 3-2), which repeated by symmetry forms a square, which in turn repeated by symmetry or rotation, either way, forms the pattern in Fig.3-2. Repeating now halves of this last pattern on all sides, we obtain the whole pattern in foreground, which contain thus 24 EG.
Note that the ribbons or bands are not centered on their lattice lines, but displaced, in order to get their vertices on the little square in the center of the quarter
 |
|
| Fig.3-2. Lattice, EG and its circular repetition,TE, for foreground pattern in tilework 3. |
| Fig.5.16-lattice vs 10-lattice patterns. |
Rige in the Background.
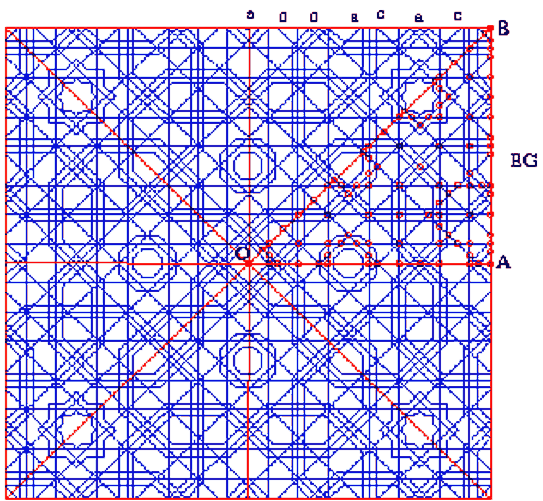 |
| Fig.3-2. Lattice, EG and its circular repetition, TE, for foreground pattern in tile work 3. |
In fig 3.3 the lattice of the background web can be seen, in small grain or resolution. The lattice is a 8-lattice, with 4 directions of angles beginning in the horizontal, in steps of a quarter of p: 0º, 45º, 90º and 135º.
This is a periodic lattice, with different - and long - periods of distance successions in the horizontal and vertical directions in one side:
...c,a,c,a,c,c,a,c,c,a,c,a,c,c,...
and, in the other side, in the oblique directions:
...a,c,a,c,c,a,c,a,c,c,c,a,c,a,c,c,a,c,a,...
being the ratio a/c the square root of 2.
The pattern presented in figs. 3-3, 3-4 is hidden by the foreground Rige, and has been reconstructed by applying the parsimony laws stated before, in a kind of geometric logic based on simplicity. In fact this pattern can still be seen under the foreground, distorted by color changes. The centers of 8 pointed stars are important references: all the vertices of foreground Rige are situated on them; in our reconstruction, therefore, in those centres, little figures - not really belonging to the pattern - have been added to guide the eye and help the design.
Without these little figures, we count only four different EE: 8-star, house, square and butterfly tie
 |
| Fig.3-5. Compound pattern in Third Tile work Panel |
Compound Figure.
When we superpose both Rige, in the due situation and proportion, fig.3-5 is obtained, showing, in a transparent way, the mutual relationship between both patterns to form the third tile work panel.
CONCLUSION
In these pages we have shown the power of our Rige model to analyze, understand, code, reconstruct and draw the actual tile work found in Islamic architecture, Iran in this case. Here we have tried to show the beauty and meanings of these patterns, which we believe strongly related to their geometrical and numerical properties. These beauty and meanings are, therefore, rational, the only way to become symbolic. It would be our pleasure to have attained this aim, becoming ourselves channels for these messages of the Tradition.
REFERENCES
ABOU-ESH, I.M. (1970) Design Concepts of Islamic Arquitecture. Beirut: Dar Al-Arabiyah.
ARDALAN, N. & BAKHTIAR, L. (1973) The Sense of Unity. Chicago: Chicago Press.
AUDSLEY, W. & AUDSLEY, G. (1968) Designs and Patterns from Historic Ornament. N.York: Dover.
BARKER, A.(ed) (1989) Greek musical Writings, II: Harmony & Acoustic Theory. Cambridge: Cambridge.Univ. Press.
BOURGOIN, J. (1973) Arabic Geometrical Pattern & Design. N.York: Dover.
BOURGOIN, J. (1977) Islamic Patterns. N.York: Dover.
BURCKHARDT, T. (1972) Moorish Culture in Spain. London: Allen & Unwin.
BURCKHARDT, T. (1976) Art of Islam. Language and Meaning. London: World of Islam Festival.
CABANELAS, D. (1988) "El Techo del Salón de Comares en la Alhambra". Granada: Patronato Alhambra.
COXETER, H.S.M. (1973) Regular Polytopes. N.York: Dover.
CRITCHLOW, K. (1969) Orders in Space. London: Thames & Hudson.
CRITCHLOW, K. (1992) Islamic Patterns. London: Thames & Hudson.
GHICA, M.C. (1977) Estética de las Proporciones en la Naturaleza y en las Artes. Barcelona: Poseidón.
GRABAR, O. (1984) Los fundamentos del arte islámico. Madrid: Cátedra.
HUNTLEY, H.E. (1970) The Divine Proportion. New York: Dover.
JAWAD al-JANAB,T. (1982) Studies in Medieval Architecture. Baghdad: Ministry of Culture & Information .
LANE POOLE,S. (1888) The Art of the Sarazens in Egypt. London: Chapman & Hall. (Repr: (1976) Lahore; Al Biruni.)
LAWLOR, R. (1982 ) Sacred Geometry. London: Thames and Hudson.
LEGADO ANDALUSÍ. (1995) El Mudéjar Iberoamericano: Del Islam al Nuevo Mundo. Sierra Nevada '95.Barcelona-Madrid: Lunwerg Editores.
MARTÍNEZ, B. (1976) "Carpintería Mudéjar Toledana". Granada: Cuadernos Alhambra,12.
NUERE, E. (1989) La Carpintería de Armar Española. Madrid: Ministerio Cultura.
NASR, S.H. (1987) Islamic Art and Spirituality. Ipswich, UK: Golgonooza.
ÖGEL, S. (1987) Anadolu Selçuklulari'nin Ta
PAVÓN MALDONADO, B. (1990) El Arte Hispano-Mulsulmán en su Decoración Geométrica. Madrid: Min. Cultura y Agencia Española de Cooperación Internacional.
PRIETO y VIVES, A. (1977) El Arte de la Lacería. Madrid: Colegio Ingen. Caminos, Canales y Puertos.
RADEMACHER, H. & TOEPLITZ, O. (1970) Números y Figuras. Madrid: Alianza.
RALEIGH, A.S. (1987) Occult Geometry and Hermetic Science of Motion & Numbers. Marina del Rey, CA: De Vorss.
SÁNCHEZ, A.. Trigonometría Rectilínea y Esférica. Lib.Romo. Madrid, 1944.
SÁNCHEZ, F.J. (1993-a) "ESCALA, Automatic Measurement of Oriental Scales". Proc. ICEMCO. Cambridge Univ. Cambridge.
SÁNCHEZ, F.J. (1993-b.) "PUERTRA: a Model of Islamic Rectilinear Interlaced Lattices". Proc. ICEMCO. Cambridge: Univ. Cambridge.
SÁNCHEZ, F.J. (1995) "A Model of Islamic Rectilinear Interlaced Lattices". Interactive Internet version: http://isfahan.apu.ac.uk/puertra4/index.html
SPELTZ, A. (1959) The Styles of Ornament. N.York: Dover.
STEWART, I.; GOLUBITSKY, M . (1992) Fearful Symmetry.Is God a geometer?. London: Penguin.
TALBOT RICE, D. (1975) Islamic Art. London: Thames and Hudson.
TROCHFORD, T. (1995) "Visit Isfahan" Internet Site:http://isfahan.apu.ac.uk/
http:www.anglia.ac.uk/~trochford/isfahan.html
VARDERBROECK, A. (1972) Philosophical geometry. Rochester, VT: Inner Traditions International.
VOROBIOV, N.N. (1974) Números de Fibonacci. Moscow: Mir.
WILSON, E. (1988) Islamic Designs. N.York: Dover.
Vuelta al Principio Última
actualización: miércoles, 05 de septiembre de 2018 Visitantes: