Esta página está en construcción: perdonen los errores y temas inacabados.
This page is being developed: I am sorry for errors and unfinished subjects.
Pseudocardioide (forma parte de Enegramas)
Un hallazgo curioso de estas representaciones de un cociente en
una cierta base es la aparición de unas figuras en forma de hoja o
 corazón, simple, doble o
múltiple en general, para valores elevados de n y b.
corazón, simple, doble o
múltiple en general, para valores elevados de n y b.
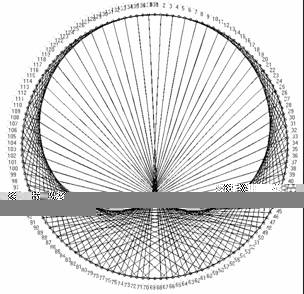
En efecto, sorprende en la representación aludida la aparición gradual de una figura en forma de corazón u hoja de árbol a medida que aumentamos el denominador de la fracción y paralelamente la base de numeración. La hoja se mantiene para una diferencia de 2 entre ambos, a favor de la base (b - n = 2). Si la diferencia es 3, aparecen 2 lóbulos, como una célula dividiéndose por mitosis. Si aumentamos la diferencia aparecen más lóbulos, siempre uno menos que esa diferencia, y la figura deviene una especie de mórula o mora. Las connotaciones orgánicas saltan pues a la vista y sugieren una nomenclatura apropiada.
Es decir, siempre no, porque las relaciones entre b y n son más complejas. Aquí la divisibilidad juega un papel primordial, con ventaja para los primos, que aparecen aquí como consistentes y generadores de formas, mientras que los números no primos, ocasionan degeneración de esas formas.
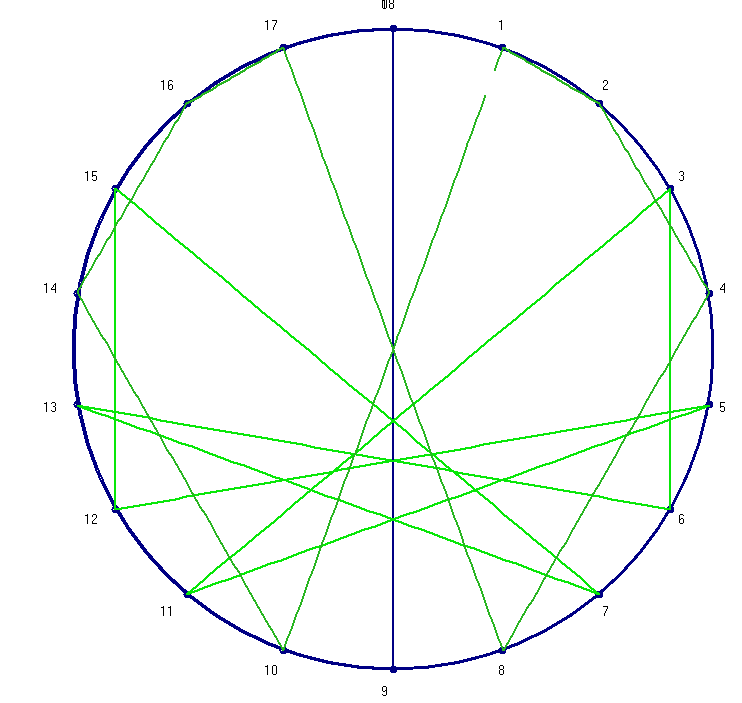
Se observa en seguida que esas figuras son los lugares geométricos de las intersecciones de todas las cuerdas que unen los puntos correspondientes a los cocientes (o restos) contiguos o sucesivos. En la figura adjunta para el par 17-19 se aprecian claramente dos cuerdas sucesivas y esa intersección, junto con un esbozo aproximado de la antedicha hoja.
Esta observación nos permite hallar su ecuación, ya ese lugar geométrico es precisamente la envolvente de esas cuerdas, que son una familia dependiendo de un parámetro, en este caso el cociente, considerado como variable, que llamaremos i. Recordemos que hemos llamado d al cociente entero de dividir la base de numeración b por el número de puntos, n.
d = b mod n
Su ecuación se consigue como es sabido, eliminando este parámetro entre la ecuación paramétrica de la familia de cuerdas y su derivada respecto al parámetro, que es i.:
F (r,q, i)
F 'i (r,q, i)
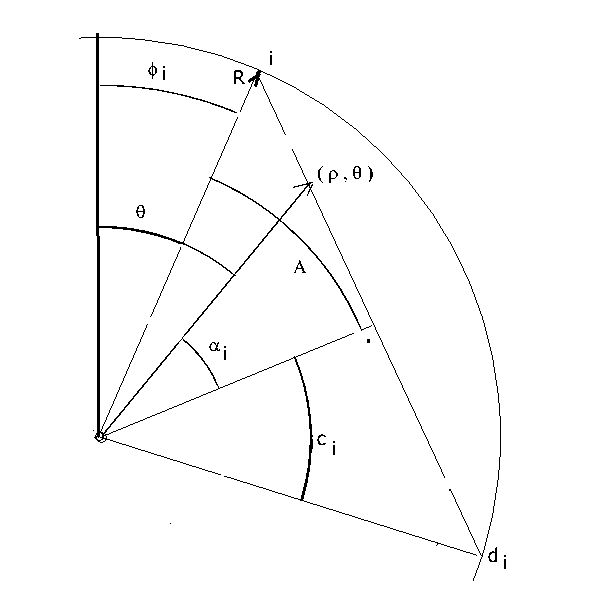 Par ello planteamos una propiedad que todas las cuerdas cumplen, lo cual las
define, es su ecuación colectiva. Y esta propiedad es que la proyección del un
punto de la cuerda sobre la flecha es constante e igual a ésta.
Par ello planteamos una propiedad que todas las cuerdas cumplen, lo cual las
define, es su ecuación colectiva. Y esta propiedad es que la proyección del un
punto de la cuerda sobre la flecha es constante e igual a ésta.
Haciendo ( d-1)p/n = c y ( d+1)p/n = c'
r cos (c' i - q) = R cos c i
- r c' sen ( c' i - q) = - R c sen c i
Dividiendo las ecuaciones eliminamos r , y elevándolas al cuadrado y sumándolas eliminamos q con lo que obtenemos las ecuaciones paramétricas de ambas variables, siendo el parámetro i el orden del cociente en la circunferencia. Ello nos conduce a las ecuaciones paramétricas de nuestra curva:
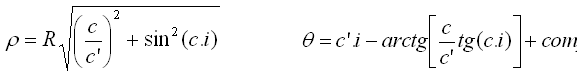
o, en función de a=(d-1)/2, a’=(d+1)/2 y fi = (2p/n) i :
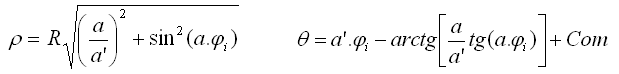
que podemos poner e función únicamente de d:
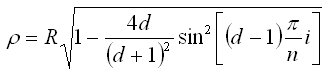
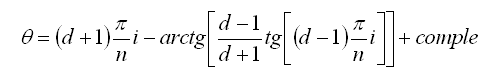
Com (o comple) es un complemento que vale p radianes (180º) cuando sin c.i y tg c.i tienen igual signo (es decir, en el primer y tercer cuadrantes del ángulo c.i que equivale a valores de i comprendidos entre 0 y 90ª y 180ª a 270ª), y es nulo cuando es opuesto (segundo y cuarto cuadrantes).
Tal cual está, la curva está definida únicamente para valores enteros de i, es decir, es una curva de puntos, discontinua. La eliminación de i nos proporciona una curva que podemos extender a cualesquiera valores reales del ángulo y por lo tanto del radio. Nos aproximamos a esa curva continua elevando los valores de b y n aunque manteniendo el valor de d.
Pese a su complicado aspecto, la ecuación es sencilla. Veamos la variación del radio r : es máximo para un valor nulo del seno bajo raíz, en cuyo caso vale R. Y es mínimo cuando el seno adquiere un valor máximo, que es 1, en cuyo caso r = R(d-1) /(d+1), un valor que tiende a 1 cuanto mayor es d, y que vale 1/3 y 1/2 para d = 2 y 3, respectivamente. Y ¿cuantas veces toma ese valor máximo y mínimo?, tantas veces cuanto valga (d-1), porque es ese caso para i pasando de 1 a n, la circunferencia completa, el valor del ángulo bajo seno vale 2p, d-1 veces (explicar!)
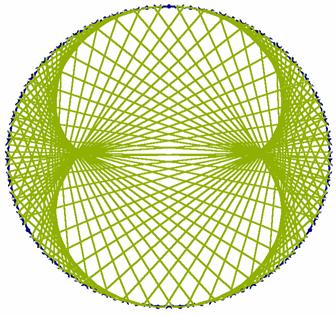 |
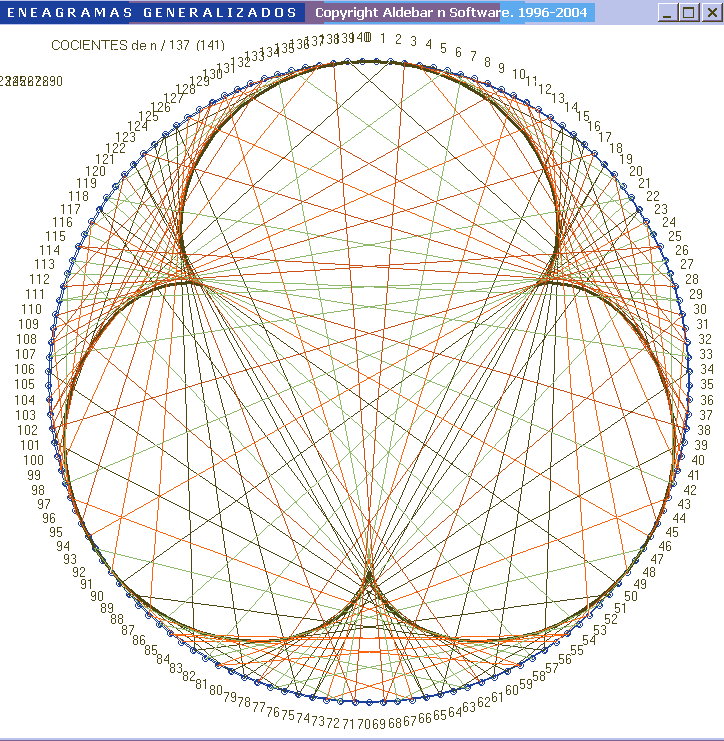 |
| Enegrama y peudocardiodes para 137140 y 11371140 . Hay d-1 = 3-1= 2 lóbulos | Enegrama y peudocardiode para 137141 Hay d-1 = 4-1= 3 lóbulos |
Así que habrá d-1 lóbulos en nuestra curva, como puede observarse en las figuras, y ello es independiente de n, el divisor, sólo depende de la relación b mod n. (el resto de su división entera). Por ejemplo, en la figura se representa el caso 137-141, d = 4.
Nótese que la curva está compuesta de n puntos aislados y sólo cuando n se hace muy grande la curva pasa a ser casi continua.
Por cierto, es interesante este acercamiento de líneas de puntos a una continua: la percepción de la forma, la gestalt, adivina el límite mucho antes de llegar (es una metáfora). Esta percepción guía la intuición matemática, titila como avisándonos de que 'aquí hay algo'.
Esto es lo que nos ocurrió a nosotros en este y muchos otros temas.
Programación
Codificación de las fórmulas anteriores que dibuja las curvas que aparecen en esta página:
'ECUACIÓN: |
| Rutina de dibujo de las pseudocardiodes, en Visual Basic |
Cardioide versus pseudo.
Hemos dado el nombre de pseudocardioide a nuestra curva debido a su forma. ¿Pseudo?. Observamos que para d=1 el coeficiente del seno al cuadrado bajo raíz es 1, y el seno es 0, con lo que el radio es constante y el ángulo coincide con el ángulo del punto (2PI/n). La pseudocardioide degenera en el propio círculo.
Hemos dado el nombre de pseudocardioide a nuestra curva debido a su forma. ¿Pseudo?. Observamos que para d=1 el coeficiente del seno al cuadrado bajo raíz es 1, y el seno es 0, con lo que el radio es constante y el ángulo coincide con el ángulo del punto (2PI/n). La pseudocardioide degenera en el propio círculo. Para
d=2, c=p/n, c'= 3p/n y c/c'= 1/3 , o bien a=1/2, a’=3/2, a/a’=1/3, y, recordando que (2p/n).i=fi
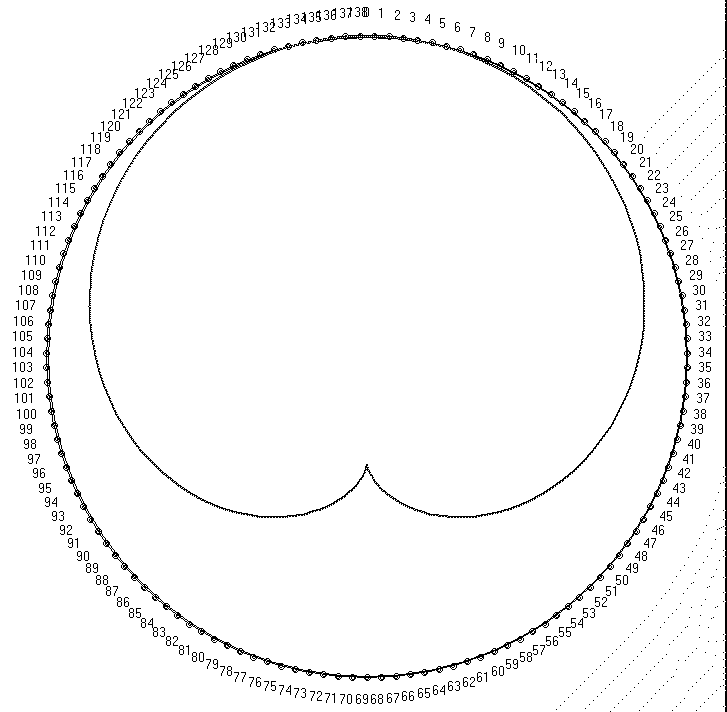
se obtiene, en este caso:
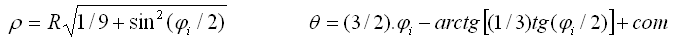
'
|
|
La pseudocardioide para d=2 en el caso 137 (139) |
pero la cardioide tiene por ecuación: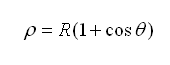 de modo que nuestra curva
no es una cardioide incluso cuando d=2. En particular la cardioide pasa
por un valor del radio nulo (cuando Teta vale PI), mientras que nuestra curva
sólo llega a 1/2 y esto para el caso d=2
de modo que nuestra curva
no es una cardioide incluso cuando d=2. En particular la cardioide pasa
por un valor del radio nulo (cuando Teta vale PI), mientras que nuestra curva
sólo llega a 1/2 y esto para el caso d=2
Peudocardiodes entrelazadas.
Para valores adecuados, nuestra pseudocardioide se entrelaza, crea vueltas, se introduce dentro de sí.
(continúa)
Vuelta al Principio Última
actualización:
Thursday, 21 de February de 2013 Visitantes: