Modelo esquemático de arco (forma parte de Arqueria)
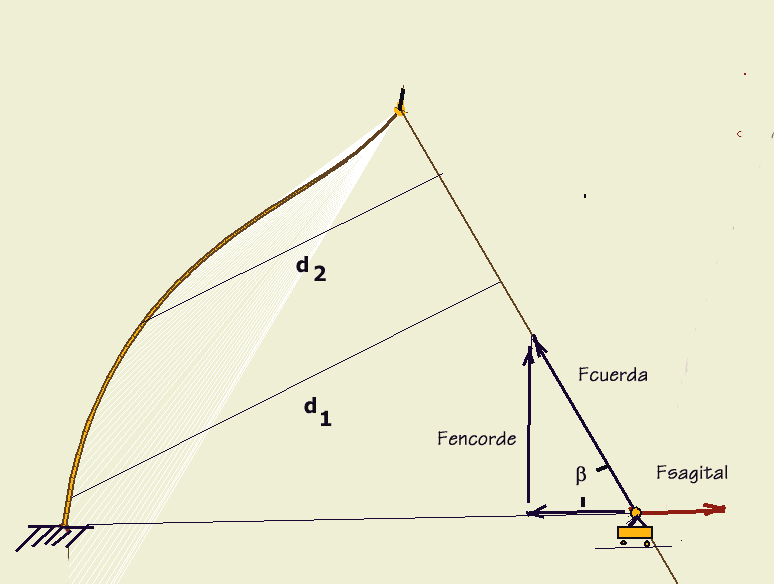
El modelo reflejado en la figura 1 puede simplificarse hasta llegar al de la figura 2.
Se cuenta en el esquema cómo todo el movimiento de la pala (que representamos recta) toma como eje el principio de la parte móvil (situado en el arco real un poco más arriba de l / 3 del cuerpo, aproximadamente a unos 50 cm. del encorde. De modo que las longitudes de pala y de cuerda se consideran fijas (la cuerda con más razón)
 |
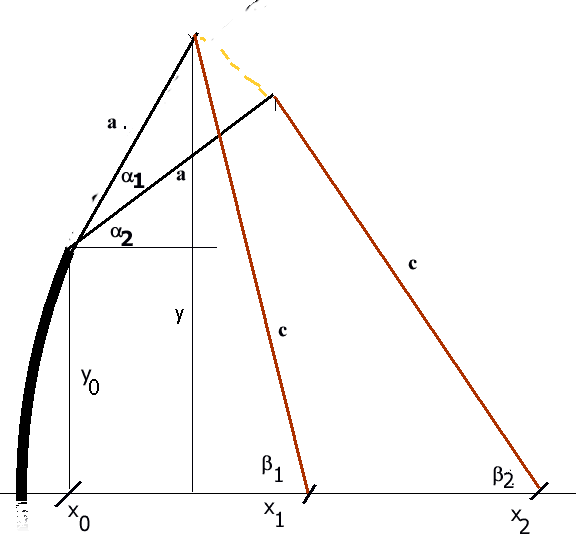 |
| esquema curvilíneo | esquema rectilíneo |
Rápidamente obtenernos relaciones simples entre la apertura angular de la pala y posición del encoque de la flecha, x, en todo momento, en efecto, tomando como origen de abscisas la vertical del extremo del cuerpo del arco. x0.:
a . cos(a) + c . cos (b) = x yp +a . sen(a) = c . sen(b)ecuaciones que nos permiten poner x en función de a, ángulo girado por la pala, de longitud (recta en el esquema) a. El cuerpo acaba a una altura yp y el ángulo b limita el valor de x para b = p /2, cuerda vertical y final del recorrido (si c es inextensible, lo que aceptamos en el esquema).
Eliminando b entre ambas ecuaciones obtenemos la posición de flecha x en función de a como deseábamos.
x = a . cos(a) + " [c2- (yp - a .sen(a) )2 ]
(donde " actúa como signo de raíz cuadrada). Aparecen aquí las tres longitudes fundamentales, a, arco, c, cuerda, y, cuerpo. La distancia de cuerpo a x0 es irrelevante en cuanto a la mecánica del tensado: sólo interviene como soporte o limitador de longitud de flecha.. Podemos reducir esas tres parámetros a 2 si usamos, como es natural las razones o cocientes de dos de ellas a una tercera, con lo que así normalizamos los cálcylos y conclusiones. Podemos dividir todas las longitudes por c, cuerdas o por a, pala. La distancia x de encoque, queda también normalizada con igual criterio, claro.
El radicando debe ser positivo o nulo, con lo que
c > yp - a . sen (a0 ) o sea, a . sen (a0 ) > yp - c
Conocida la posición x podemos encontrar su velocidad y aceleración derivando respecto al tiempo, para lo que hay que conocer la expresión de a en función de ese tiempo.
Ahora bien, si aceptamos que la fuerza que opera sobre la pala depende de su desplazamiento respecto su posición inicial, precisamente el ángulo a, podemos llegar a conocer el tipo de esa dependencia, una función como
f = k a
que podemos imaginar como un resorte que sujeta la pala a un punto fijo, por ejemplo, una prolongación del cuerpo. Observamos que la función es similar a la de un péndulo, y de hecho, a un péndulo se asemeja nuestro esquema si invertimos la figura y colocamos el ángulo a1 hacia abajo. Y como en el péndulo, la ecuación es aproximada para pequeños a, y esto, dependiendo de la colocación y dirección del resorte (sobre un arco de radio mayor o menor, a compresión o tracción, sobre una cuerda, otra dirección, etc.).
Esta ecuación es la muy conocida del péndulo simple, Su solución es una combinación lineal de las funciones trigonométricas seno y coseno, cuyas segundas derivadas son iguales a las funciones primitivas salvo por un signo menos que queda incluido en la constante de proporcionalidad k.:
Esa fuerza es la que propulsará una masa de inercia m (que proviene de la pala, cuerda y flecha, pero que ahora no conocemos) con una aceleración z.
m z = k a
expresión en la que todas las cantidades salvo k (constante elástica de un resorte) son variables con el tiempo:.
m(t) . z(t) = k . a(t)
y siendo la masa m una cantidad que recoge las masas inertes de palas, cuerda y flecha en una forma por determinar.
Vuelta al
Principio
Última
actualización:
Thursday, 21 de February de 2013 Visitantes: